Mystery of the First 1000 Prime Numbers

This work is licensed by its author, Gary William Croft, under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Return to www.primesdemystified.com Home Page

This work is licensed by its author, Gary William Croft, under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
Return to www.primesdemystified.com Home Page
"In the ideal world of numbers and shapes, strange coincidences usually are clues that we're missing something. They Suggest the presence of hidden forces at work." – Steven Strogatz, The Joy of X: A Guided Tour of Math from One to Infinity
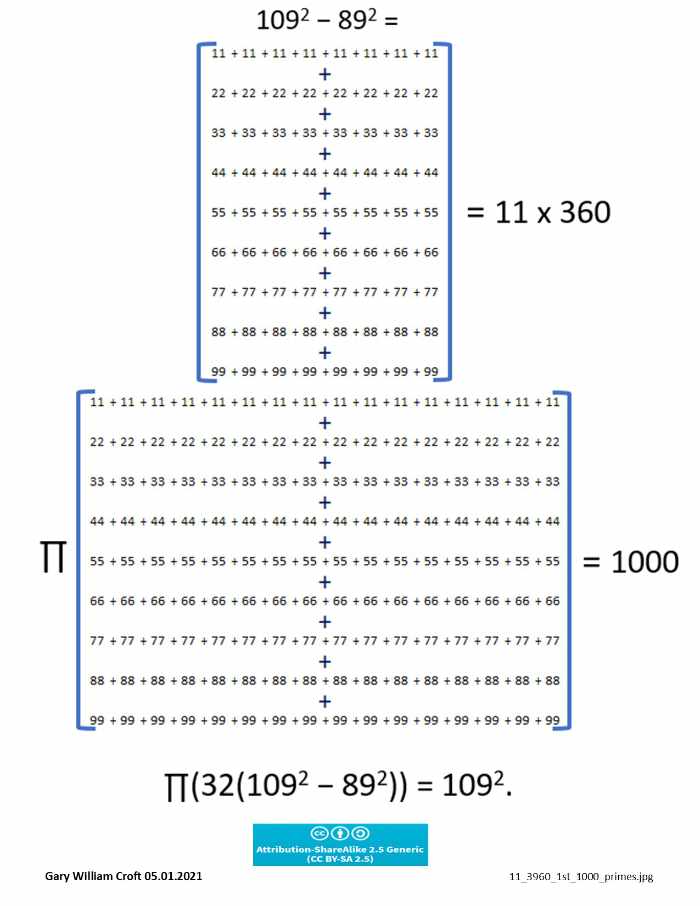
The first 1000 prime numbers are silently screaming: "Pay attention to us, for we hold the secret to the distribution of all primes!" We heard the call, and with 'strange coincidences' leading the way have discovered compelling evidence that the 1000th prime number, 7919, is the perfectly positioned cornerstone of a mathematical object with highly organized substructures and stunning reflectional symmetries. This object is dually enveloped by 892 = 7921 and 7920 = 22 x 360 in conjunction with 1092 − 892 = 3960 = 11 x 360 (while mindful that both 1/89 and 1/109 have the Fibonacci sequence secreted in their decimal expansions). And we note the astonishing fact that primes 11 + 89 + 109 + 7919 = 8128, the fourth perfect number, the first three of which are 6, 28, and 496.
And so we give you:
"To excavate a pyramid is the dream of every archaeologist." – Sarah Parcak
It is no accident that this page's header image is of a 4-sided pyramid. What this iconic geometric form has to do with the first 1000 prime numbers will become evident toward the bottom of this page where we excavate the 'One Grand Pyramid' aka 'Tomb of the First 1000 Primes.'
For now we will be coy and state that the secret of the pyramid lies with two 4-times triangular numbers: The first, 2112 (4 x triangular number 528), equates to the total number of elements used to construct the pyramid, which is subdivided into its four lateral faces comprised of 528 elements each in the form of 32 cascading triangular numbers.
These N = 0,1,2,3,... construction elements are then bijected with and serve as index numbers for our domain, defined as natural numbers not divisible by 2, 3, or 5. And so it is that 2112, index number of the 1000th prime number as a member of this domain, is the terminating element of the pyramid bijecting 7919, i.e., 2112 and 7919 have a one-to-one correspondence.
The second pivotal number, 112, is the element count of the pyramid's pyramidion or capstone. We interpret 112, which is 4 x triangular number 28 (the 2nd perfect number), as a string reflecting the first three digits of the Fibonacci sequence, and representing 1+1=2, the most fundamental of so-called 'fundamental dyads.' The index numbers of the set of natural numbers not divisible by 2, 3, or 5 populating each of the capstone's four faces incrementally cascade 7 triangular numbers (1, 3, 6, 10, 15, 21, 28) for a total element count of 28. The number 28, aside from being triangular and perfect, is the sum of the first 5 primes (2 + 3 + 5 + 7 + 11 = 28) and the sum of the first 7 natural numbers (1 + 2 + 3 + 4 + 5 + 6 + 7 = 28).
Introducing a capstone into this model, as if alluding to the Great Pyramids of Giza and their sacred pyramidions (speculated to have originally been gold covered), will be greeted with incredulity by many. That's fair. For the record, this model was developed without any conscious thought given to possible parallels with Egyptian pyramids until after the fact–and then only in the form of idle curiosity (which, by the way, we've yet to fully satisfy).
We want it known that the number 112 emerged relentlessly from the data. The fact that both 112 and 2112 are 4-times triangular numbers, and that 2112 is a palindromic form of 112 were clues prompting 100's of experiments that ultimately led to exposing 112's role in building a pyramidal geometry. Regardless, we believe that once you've 'grocked' the beautiful family of ratios, digital root symmetries and triangular number progressions your skepticism about equating a capstone with the distribution of prime numbers will retreat ...
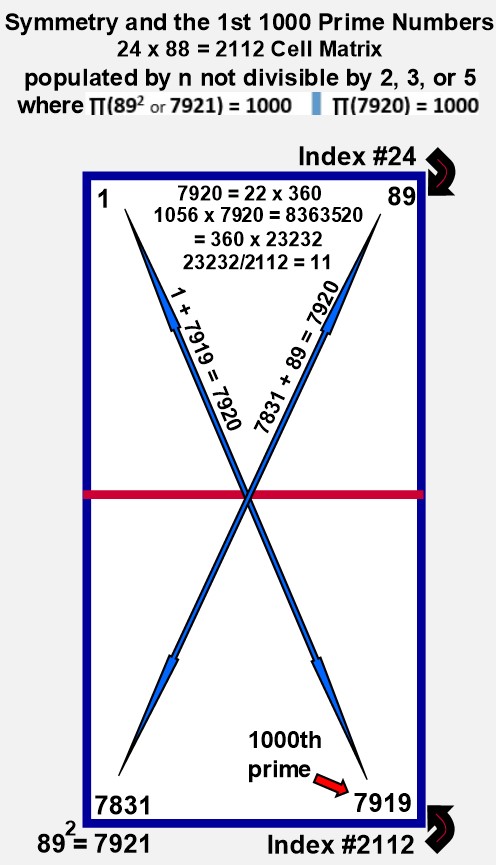
We lay the foundation for the One Grand Pyramid by providing an exhaustive list of data points employing the Prime Spiral Sieve telescoped to modulo 90 and a corresponding 24 x 88 = 2112 cell matrix–the width reflecting the period-24 digital root of this domain, and 2112 being the index number of the 1000th prime number as a member of this sequence. Also note that every quadrant of the matrix (22 of 88 rows = 528 elements) is equivalent to one lateral face of our pyramid.
And here are three more intriguing correspondences between 2112 (pyramid) and 112 (pyramidion): 1) The analytical matrix is 24 x 88 = 2112; while 24 + 88 = 112; 2) 2112/112/6 = 22/7 (a commonly used equivalent for pi) and it follows that 6(22/7)112 = 2112, while 528/28/6 = 132/7/6 = 22/7; and, 3) Primes (11 + 13) x (41 + 47) = 2112, while 11+13+41+47 = 112.
It was the challenge of finding an object that will accommodate 2112 elements while preserving the digital root reflective symmetry fundamental to our defined domain (numbers not divisible by 2, 3, or 5) that led to the perfect symmetry achieved when the 2112 elements are evenly distributed to the four equilateral sides of the One Grand Pyramid, configured in the form of counter-balancing polarities, with 2112/2 = 1056 pairs summing to 7920 (and note that 7920−1 = 7919, the 1000th prime, and 7920+1 = 892). And thus a rectangle is transformed into a beautifully proportioned pyramid.
Before getting to the data, the graphic below prefigures the pyramid to come:

And here are some tantalizing related factoids:
Plugging the 1000th prime, 7919, into the formula for triangular numbers, n(n+1)/2, gives us:
7919(7919+1)/2 = 31,359,240 = 7919 x (1092 − 892);
and every one of the One Grand Pyramid's thirty-two steps sums to a multiple of (1092 − 892) = 3960.
(And, keep in mind that 3,6,9 and its permutations are fundamental to the rotating symmetry groups generated by this domain's factorization algorithms.)
"Mathematics grows when it finds new objects to explore and new structures that capture some of the most important relationships — between numbers, equations and shapes." – Kevin Hartnett, "The Mystery at the Heart of Physics That Only Math Can Solve," Quanta Magazine, June 10, 2021
The first three primes (2, 3, and 5) are set aside in this mathematical model (albeit accounted for in the grand total), given 1) they are the only prime numbers not members of our defined domain (the set of natural numbers ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30), and b) they and their primorial, 30, are nonetheless present given they form the structure within which the 8-dimension (mod 30) and 24-dimension (mod 90) factorization algorithms described on this site operate.
Our specified range for this analysis thus begins with 1 and terminates with 7919 (the 1000th prime number), and is circumscribed by two numbers:
7920 (which = 22 x 360 = 892 − 12) and,
7921 (which = 892).
Using the standard notation to represent counts of primes from 1 to x:
π(7920) = 1000 and π(892) = 1000. (The reason we’ve presented two (seemingly redundant) counting ranges will become evident.)
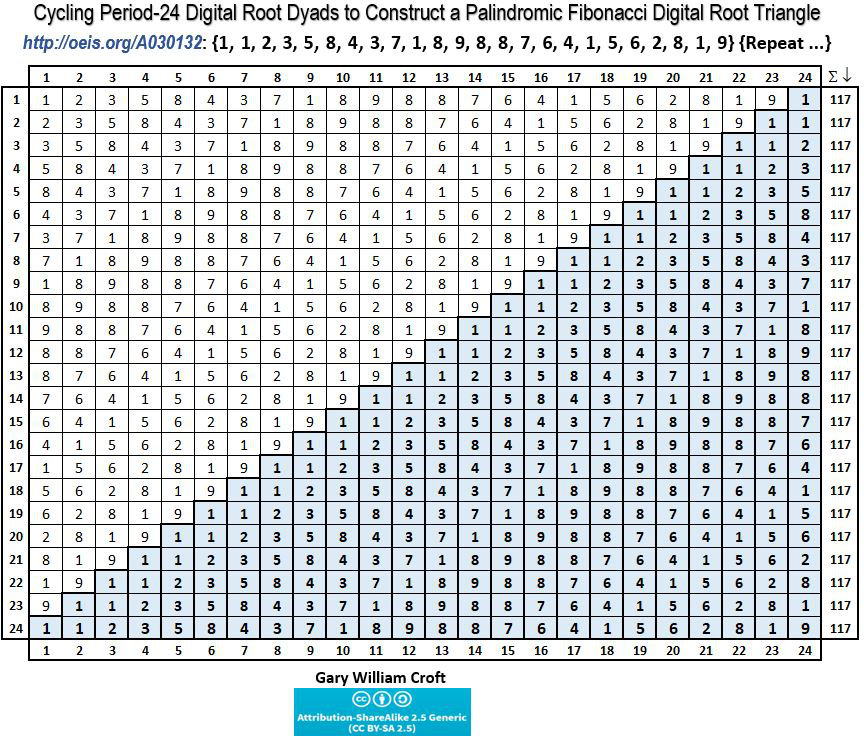
Study the relationships detailed below and you'll discover a palindromic spine concatenating from another form of the 'fudamental dyad,' 11, aka Fibo2, (viz., 11, 22, 33, 44, 55, 66, 88, 121, 242, 343, 484, 2112, 23232, 69696), vertical and horizontal reflectional symmetry composed of prime numbers (especially the 242 'Mirror Prime Pairs'), and other features that suggest this mathematical object is worthy of further study. For example: The myriad ways number 24 and its square, 576, play out dimensionally in this space are truly remarkable (and it's likely not a coincidence that the highly composite number 360 has 24 divisors).
The diagram below captures the basic dimensions of our analytical matrix, followed by a rather long list of its intriguing features (which many of you will choose to skim). Then the fully populated matrix is presented, showing row and additive sum totals for primes (hi-lited in black). After that, you'll find a graphical "footprint" of the 484 prime numbers between 1 and 7920 (exactly 112 + 112 on each side!) that form 242 Mirror Prime Pairs, or what might better be called Reflectional Symmetry Primes.
[Note: The cumulative sum and indexing formulae referenced below can be found on a page devoted to them, here: Cumulative Sum and Indexing Formulae.]
Also, be warned that you'll find a certain amount of annoying redundancy in the data compilation below. This was done deliberately to expose particularly interesting juxtapositions and associations. And note that 576 has been 'boldened' to emphasize its importance. And one can't help but wonder if there's a connection between the 88-unit dimension of this object and the 88 pitches of a modern piano, especially when you consider the connection the One Grand Pyramid and related Triangular Wave have to 3960 Hz–the 9th harmonic of fundamental frequency 440 Hz.
As you scan the list below you'll occasionally encounter what we're calling 'iterative digit division' (you can think of it as a corollary to 'iterative sum of digits' that defines digital root). For example, the cumulative sum of n not divisible by 2, 3, or 5 from 1 to the 1000th prime (7919) = 8,363,520. To calculate its iterative division root we get 8/3/6/3/5/20 = .00148148 ... (You'll note that, because zero is undefined, all zeroes adhere to the first non-zero digit preceding them.).
Here's a quote to keep in mind while scanning these data:
"Mathematicians have long wondered at the haphazard way in which the primes are sprinkled along the number line from one to infinity, and universality offers a clue. Some think there may be a matrix underlying the Riemann zeta function that is complex and correlated enough to exhibit universality. Discovering such a matrix would have 'big implications' for finally understanding the distribution of the primes ..." Natalie Wolchover, "In Mysterious Pattern, Math and Nature Converge," Quanta Magazine, 02.05.2013




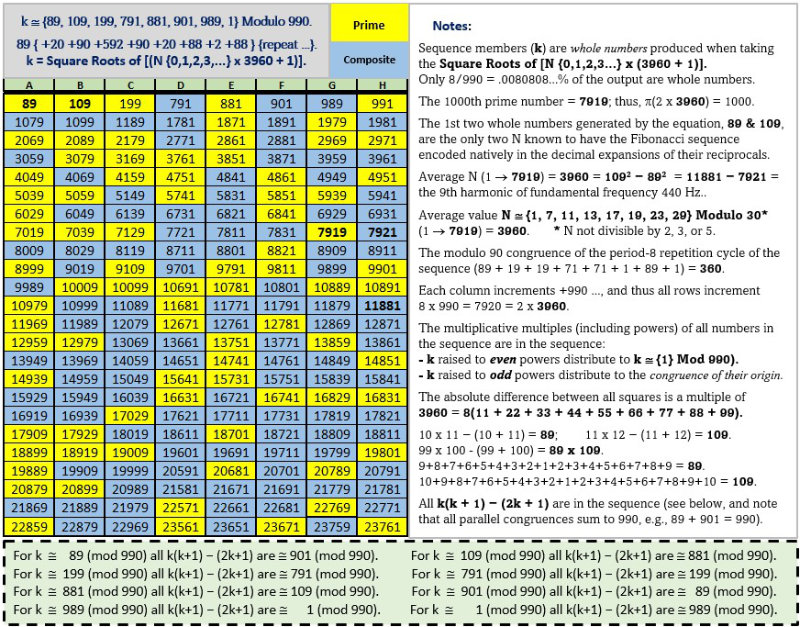





Here is the matrix under discussion:

Below is an image reflecting the "Mirror Prime Pairs" referenced above. Every pair is evenly divisible by 90 and has additive digital root sum = 9. Given the key role the number 11 plays in the structure of this matrix, it's likely not a coincidence that each side has 112 + 112 = 242 of these primes:
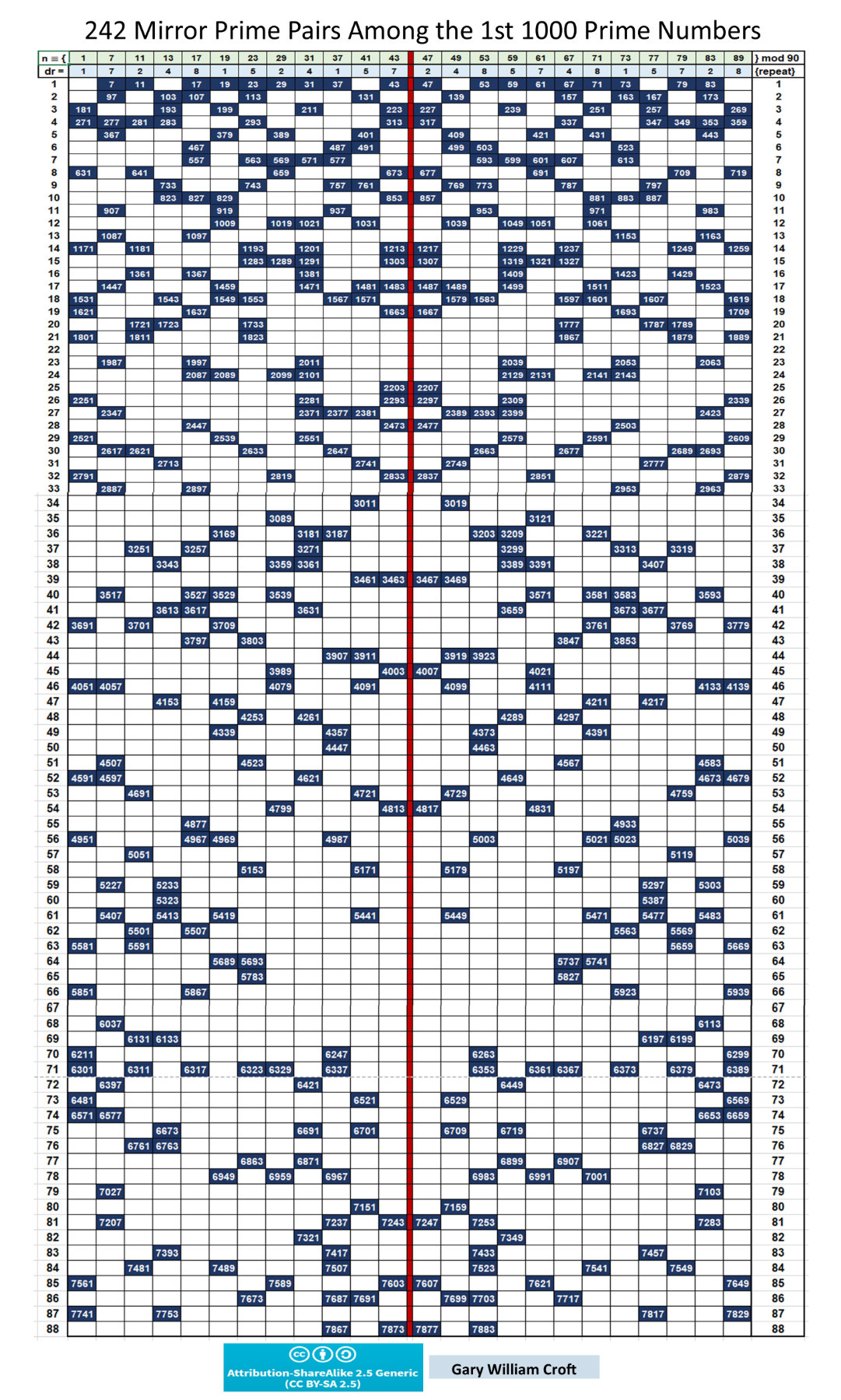

"Mathematics makes the invisible visible." – Keith Devlin, The Language of Mathematics
At the top of this page we declared that the first 1000 prime numbers are 'entombed' in a beautifully proportioned pyramid. To support this claim we offer the somewhat Archimedean construction below. We're tempted to call it the Tomb of the First 1000 Primes, but prefer the pun in 'One Grand Pyramid.'
As we've already alluded, to lay the foundation for a bijection with numbers not divisible by 2, 3, or 5, each of the pyramid's four lateral faces is constructed from a 32-step triangular number progression (oeis.org/A000217: a(n) = n(n+1)/2 ...). By definition, each triangular step is equilateral. In addition, every step dyad, starting with 1+3 = 4, sums to a perfect square, and thus each face of our pyramid cascades 12 thru 322. (Note that 4 x 32 = 128 = the perimeter of the square base which has an area of 322 = 1024 = 210. Which is to say that the pyramid's perimeter, 128, equals the number of triangular numbers employed in its construction.)
The four faces of our pyramid additively cascade 32 four-times triangular numbers (oeis.org/A046092: a(n) = 2(n+1) ...). These include Fibo1-3 equivalent 112 (rooted in T7 = 28; 28 x 4 = 112), which creates a pyramidion or capstone in our model, and 2112 (rooted in T32 = 528; 528 x 4 = 2112), which is the index number of the 1000th prime within our domain, and equals the total number of 'elements' used to construct the pyramid. Or, using the textbook way to visualize triangular numbers, 2112 = the total number of billiard balls filling the four faces, which in our case will be dually populated with natural numbers 1, 2, 3, ... and their associated numbers not divisible by 2, 3, or 5 in a 4-fold progression of perfect squares descending the faces of the pyramid.
The table below shows the telescopic progressions of triangular, 4-times triangular numbers and cascade of perfect squares that populate the pyramid's faces.
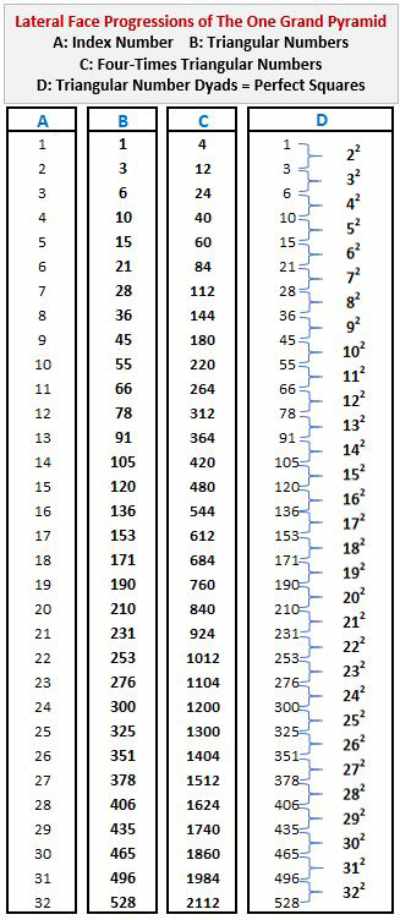
Both 112 and 2112 contain the 'fundamental dyad' 1+1 = 2 (which we featured earlier in this section). They give us a curious equation (employing iterative digital division), (2/1/1/2)(2112-112)(1/1/2) = 1000.
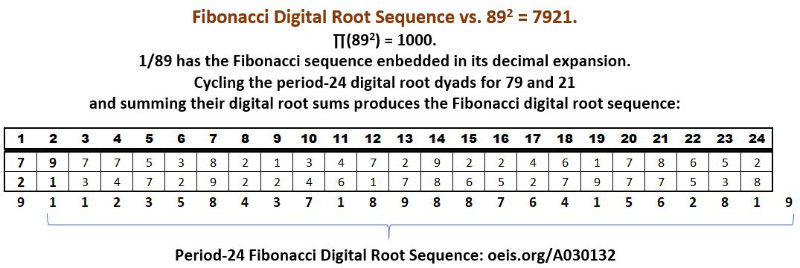
Speaking of iterative digital division–a powerful tool for exposing structure–we get this astonishing equation: iteratively dividing the digital roots of the first 12 Fibonacci numbers times the divisively iterated 1000th prime, 7919, times 3604 gives us 1000. Keep in mind that the first two and last two digits of the Fibo sequence below, 11 and 89, sum to 100; that 89 is the 11th Fibo number; that there are 1000 primes between 1 and 892; and that 89 has the Fibonacci sequence embedded in its decimal expansion:
1/1/2/3/5/8/4/3/7/1/8/9 x 7/9/1/9 x 3604 = 1000.

The graphic below shows the ranges of the numbers congruent to {1, 7, 11, 13, 17, 19, 23, 29} mod 30 populating each of the lateral faces along with their index numbers:
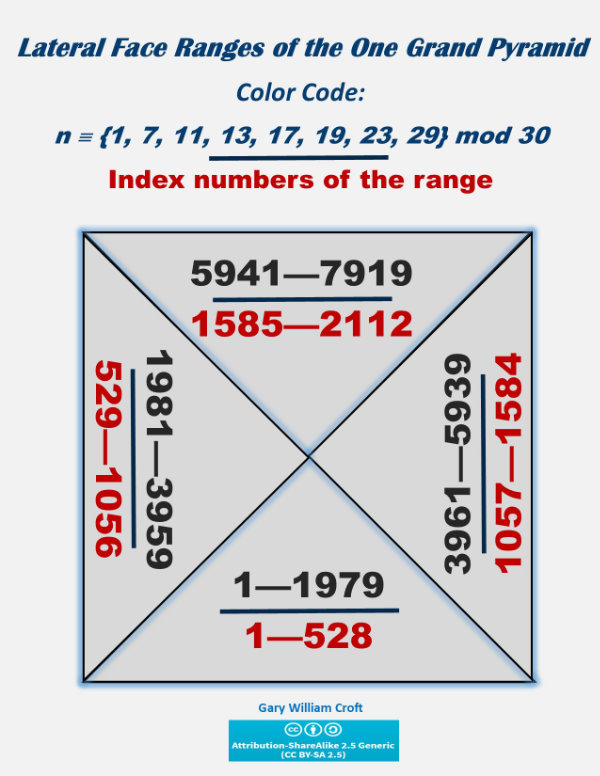
Next we focus on the pyramidion exclusively. We've populated it–and by extension this applies to the entire pyramid–in such a way as to achieve reflectional symmetry in the form of bilateral 7920 sums. The pyramidion is constructed from 56 such dyads, while the frustum accounts for the remaining 1000, for a total of 1056 x 7920 = 8,363,520 (which, of course, is the sum of the 2112 elements populating the pyramid).
The pyramid possesses 32 telescopically expanding steps (the first 7 of which constitute the pyramidion): The 1st (top) step has 4 elements, the 2nd 8 elements, the 3rd 12 elements, ... Given the symmetry of the bilateral dyads summing to 7920, and that 7920 = 15 x 528, it follows that every step of the pyramid sums to a multiple of triangular number 528. For example: Step 1 = 1 + 1981 + 7919 + 5939 = 15,840 = 7920 x 2 = 30 x 528, and amazingly 8,363,520 = 528 x the sum of Step 1, 15,840. And then we see that 56 x 7920 (additive sum of the pyramidion's 112 elements) = 443,520 = 528 x 840, while 15,840 x 28/528 = 840 and 7920 x 28/528 = 840/2. Also, 4/4/3/5/20 x 3602 = 432. And perhaps most interesting of all the pyramidion vs. pyramid ratios and proportions are these: 443,520 = 2 x 3 x 5 x 7 x 2112 and (8,363,520 − 443,520)/7920 = 1000, which equates to ((8,363,520 − (8,363,520 x 28/528))/((1092 − 892) x 2) = 1000 (and in relation to these, recall that 8,363,520/(1092 − 892) = 2112 and 443,520/(1092 − 892) = 112. We find it remarkable that every step of the pyramid is a multiple of 1092 − 892. A related equation: the triangular number generated by 7919 (ref: oeis.org/A000217; a(n) = n(n+1)/2) = 31,359,240 = 7919 x (1092 − 892).
That said, this equation may be the most provocative of all:
1396 − (1092 − 892)/10 = 1000.
Why provocative? Because 1396 equals the total number of calculations required in our Prime Number Counting Methodology to index all composite numbers in the range 1→892. Yet another connection to 89 is that the sum of the index numbers of every one of the 1056 dyads forming the pyramid sum to 2113, which is the index number of 7921 = 892.

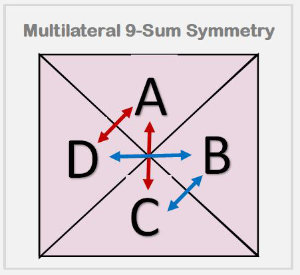
To make the reflectional and rotational symmetry more conspicuous, we've converted the numbers not divisible by 2, 3, or 5 populating the pyramidion to their digital roots. When you rotate the opposing horizontal faces (as pictured) 90° counter-clockwise, and/or the vertical faces 90° clockwise, they superimpose with identical values. And we note that the additive sum of the pyramidion's digital roots = 504, which is consistent with the ratio 9504 x 28/528 = 504 (9504 being the cumulative digital root, 1 → 7919).

Examine the above graphic and you'll discover four ways lateral and/or adjacent faces have bilateral 9 digital root sum symmetry (illustrated below):
Summarizing some of the above relationships:
8,363,520/443,520 = 2112/112 = 528/28 = 7/132.
28/528 x Pyramid Unit Sum = Pyramidion Unit Sum; 28/528 x Pyramid Face Unit Sum = Pyramidion Face Unit Sum (or Pyramidion/4).
528 x 28/528 = 28; 528 x 112/2112 = 28 (which happens to be the 2nd perfect number).
2112 x 28/528 = 112; 7/9/1/9 x 362 = 112; and, 1/90 x 28 x 360 = 112.
24 x 88 = 2112; 24 + 88 = 112.
28/112 x 2112 = 528; and, 2112/112 x 28 = 528.
8,363,520/4 = 528 x (1092 − 892) = 528 x 3960.
3960 x 28/528 = 2 x 3 x 5 x 7.
500/28 x 112 = 2000 (frustum element count).
528/28 x 112 = 2112; 2112/112 x (7/9/1/9) x 362 = 2112; 112/(7/132) = 2112; and, 1/90 x 528 x 360 = 2112.
112((1092 − 892)/(2 x 3 x 5 x 7)) = 2112.
(1092 − 892)/(528/28)/(2 x 3 x 5 x 7) = 1.
6π x 112 = 2111.1526321, while 6(3 1/7) x 112 = 2112 (3 1/7 is a commonly used approximation of pi and 528/28/6 = 3 1/7 and 528/6 = 2112/24).
28/528 x 2112/112 = 1.
And, we note that:
(2112-112)/2 = 1000.
(2112-112) x 1/1/2 = 1000.
500/28 x 112/2 = 1000.
2000/112 x (7/9/1/9) x 362/2 = 1000
(2/1/1/2)(2112-112)(1/1/2) = 1000.
(2112 − (2112 x 28/528)/2) = 1000.
(8,363,520 − (8,363,520 x 28/528))/7920 = 1000.
(7 x (4/3/2)2)2 x (7 x (5/7/6)2) x (3/60)2 x 3603/112 = 1000 (whew!).
1/2/3/4/5/6/7/8 x 112 x 360 = 1.
7/11 x 2112/112 = 12.
1/1/2 x (8/3/6/3/5/20) x 360 = 8/30 = ratio of numbers not divisible by 2, 3, or 5 to N = {0,1,2,3, ...}.
1/1/2 x (8/3/6/3/5/20) x 3602 = 96 = the number of perfect squares generated by the Prime Spiral Sieve during one complete modulo 90 factorization cycle.
112 x (1092 − 892) = 443,520 (pyramidion's cumulative sum n not divisible by 2, 3, or 5).
2112 x (1092 − 892) = 8,363,520 (pyramid's cumulative sum n not divisible by 2, 3, or 5).
1/1/2 x (8/3/6/3/5/20) x 3603 = the 5th 'Superfactorial = 1! x 2! x 3! x 4! x 5! = 34560.
2/1/1/2 x (8/3/6/3/5/20) x 3603 = 2 x 34560.
Scanning the above data, the eagle-eyed will have noticed this distinctive pattern. It speaks for itself:
528 ... 28, as in 528 x 28/528 = 28;
1056 ... 56, as in 1056 x 28/528 = 56;
2112 ... 112, as in 2112 x 28/528 = 112;
9504 ... 504, as in 9504 x 28/528 = 504;
23232 ... 232, as in 23232 x 28/528 = 1,232;
69696 ... 696, as in 69696 x 28/528 = 3,696;
8,363,520 ... 3,520, as in 8,363,520 x 28/528 = 443,520.
"The triangular numbers have important implications within both our everyday world and the world of number theory." – Edward B. Burger, PhD, An Introduction to Number Theory
Speculating beyond the pyramidal model just described, the ratios seem to suggest that this geometry can be conceived sinusoidally as a Fourier series forming continuous triangular waves that reverse polarity in quarter cycles.
For example, the 9th harmonic of the fundamental frequency 440 Hz = 3960 Hz (and keep in mind that 3960 = 1092 − 892, their relationship to the first 1000 primes covered in detail earlier in this section). Then consider that 8,363,520 (additive sum of the pyramid)/(1092 − 892) = 2112 (index # of the 1000th prime); 8/3/6/3/5/20 x (1092 − 892) x 360 = 2112; and that 443,520 (additive sum of the pyramidion)/(1092 − 892) = 112 (index # of 419, the 81st prime [as in 92, interestingly], and in turn 7919 x 28/528 = [419]; whole number part taken).
Here's a draft of what the proposed triangular wave might look like:
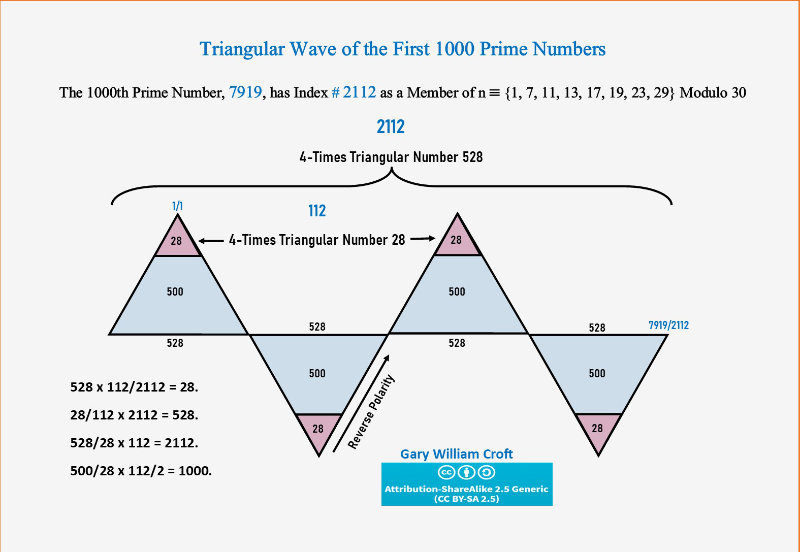
The relationship between the triangular numbers and Fibo1-3, 112 (the element count of our pyramidion), is further illuminated by this period-30, modulo 8 generated palindrome:

And the following example also exposes hidden structure:
π(7920) = 1000; 7919 is 1000th Prime.
There are 243 prime pairs among the first 1000 primes that sum to 7920, where 243 x 7920 gives additive sum 1,924,560 (and we note that 7920 = 22 x 360 = 2(1092 − 892), which equates to 1,924,560/(2(1092 − 892) = 243.).
Additive Sum n 1, 2, 3, ... (1 - 7919) = 31,359,240.
Additive Sum n ≌ (1, 7, 11, 13, 17, 19, 23, 29} modulo 30 (1 - 7919) = 8,363,520.
Now consider this:
1 x 9 x 2 x 4 x 5 x 60 = 21,600 = 60 x 360 = 50 x 432.
3 x 1 x 3 x 5 x 9 x 2 x 40 = 32,400 = 90 x 360 = 75 x 432.
8 x 3 x 6 x 3 x 5 x 20 = 43,200 = 120 x 360 = 100 x 432.
Here we incorporate the formula for k = the cumulative sum (1-n) for n ≌ {29} modulo 30; namely, k = (n+1)2 * 8/30/2.
[(7919+1)2 * 8/30/2]/2112/11 = 360.
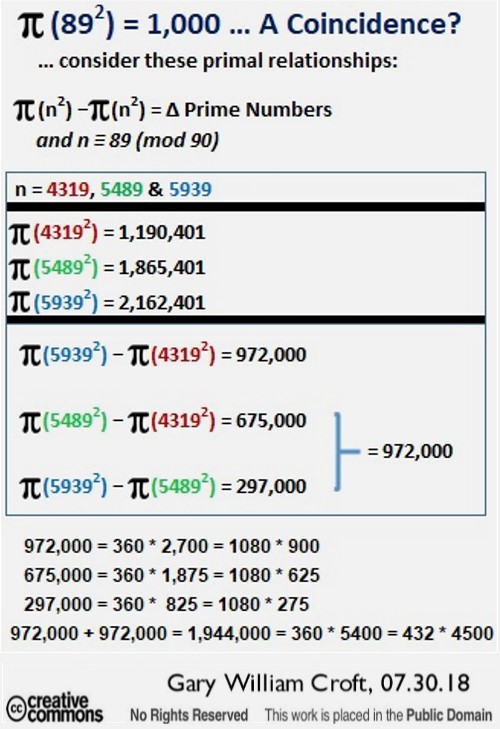
In the following provocative study we sieve the delta differences in prime number counts between the squares of n congruent to {89} modulo 90 and test their divisibility by 360 and 1000 (and we find especially interesting those deltas evenly divisible by both):

Focusing in on the deltas with divisibility by 1000, we find the following fascinating relationships:
Here are some thought provoking coincidences:

Then there are these strange coincidences:

And here's a related formulation that begs further study: [Note: In the equation illustrated below, where (89 * 8/30 +1) * (89 +1)/2 = 1113, the whole number part is not taken for (89 * 8/30 +1), unlike in the formula shown for index numbers of n not divisible by 2, 3, or 5, where whole number parts are indeed taken, e.g., 89's index number equates to 89 * 8/30 +1 = 24.]

Here we connect the power series we presented on our home page involving the first three primes to the first 1000 primes in toto:

And here, at the risk of making fools of ourselves, we leave you with an equation full of sound and fury, signifying nothing:
