The Four Cumulative Sum Formulae:
While rolling stones may gather no moss, the same can't be said when it comes to 'rolling up' numbers. These formulae expose the fact that natural numbers can possess various 'weights and measures.' They are essentially partial sum and piecewise counting functions in simplified form. They are especially powerful when used in combination to expose hidden patternization and structure.
1. Cumulative Sums (k) for Natural Numbers (n) 1, 2, 3, ...
k = (n + n2)/2.
[Note that the cumulative sums this formula generates are the triangular numbers, viz. 1, 3, 6, 10, 15, 21, 28, ... (ref: oeis.org/A000217: a(n) = n(n+1)/2 ...)]
Examples:
n = 89 (the 24th prime): k = (89 + 892)/2 = 4,005.
n = 109 (the 29th prime): k = (109 + 1092)/2 = 5,995 (and, interestingly, 4,005 + 5,995 = 10,000).
n = 7919 (the 1000th prime): k = (7919 + 79192)/2 = 31,359,240 (and note that 31,359,240 = 7919 x (1092 − 892), and that the Fibonacci sequence can be extracted from the decimal expansions of both 1/89 and 1/109).
Here's an example demonstrating how this formula, combined with others on this page, can be employed to expose deep connections:

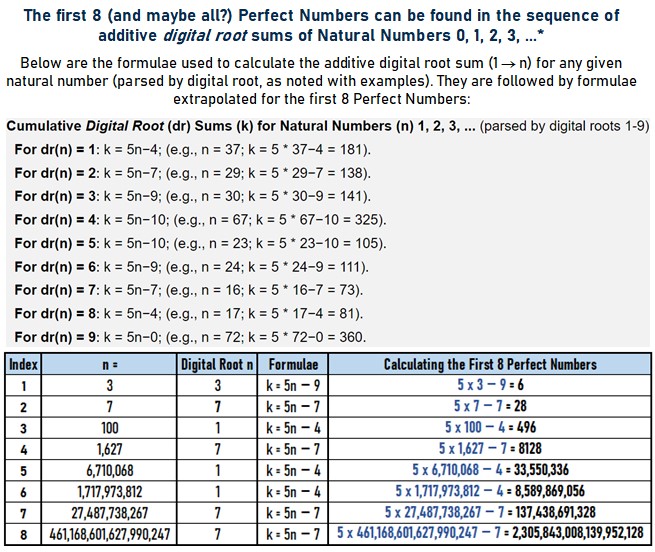
2. Cumulative Digital Root (dr) Sums (k) for Natural Numbers (n) 1, 2, 3, ... (parsed by digital roots 1-9)
For dr(n) = 1: k = 5n−4; (e.g., n = 37; k = 5 * 37−4 = 181).
For dr(n) = 2: k = 5n−7; (e.g., n = 29; k = 5 * 29−7 = 138).
For dr(n) = 3: k = 5n−9; (e.g., n = 30; k = 5 * 30−9 = 141).
For dr(n) = 4: k = 5n−10; (e.g., n = 67; k = 5 * 67−10 = 325).
For dr(n) = 5: k = 5n−10; (e.g., n = 23; k = 5 * 23−10 = 105).
For dr(n) = 6: k = 5n−9; (e.g., n = 24; k = 5 * 24−9 = 111).
For dr(n) = 7: k = 5n−7; (e.g., n = 16; k = 5 * 16−7 = 73).
For dr(n) = 8: k = 5n−4; (e.g., n = 17; k = 5 * 17−4 = 81).
For dr(n) = 9: k = 5n−0; (e.g., n = 72; k = 5 * 72−0 = 360.
The examples above were taken from the section of spreadsheet cut-and-pasted below covering the range of natural numbers 1 thru 72 (and associated cumulative digital root 1 thru 360). Prime numbers are hi-lited in yellow.
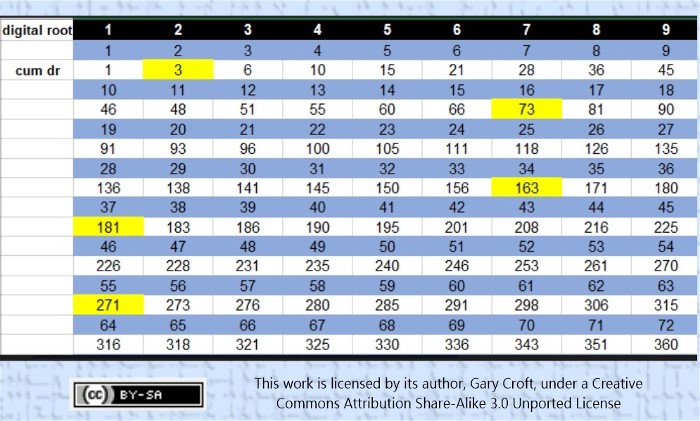
Based on this analysis, it can easily be proven that, with the exception of the first prime (1+2=3) all primes in this sequence are congruent to {1 or 73} modulo 90, and therefore all, with the exception of number 3, have a digital root of one (1). For example, in the range 1 thru 7920 there are 345 such 'cumulative digital root' primes (and of these, 171 are n ≌ {1} mod 90 and 173 are n ≌ {73} mod 90. Number 3 is the only outlier). And we note that all but the first perfect number (6) are congruent to either {28} or {46} modulo 90, thus: 28, 8128, 127438691328, and 2305843008139952128 are congruent to {28} modulo 90, while
496, 33550336, and 8589869056 are congruent to {46} modulo 90.
Further review of this sequence leads us to the conjecture that this sequence contains all perfect numbers. We've confirmed that it contains the first eight of them (see details, below).
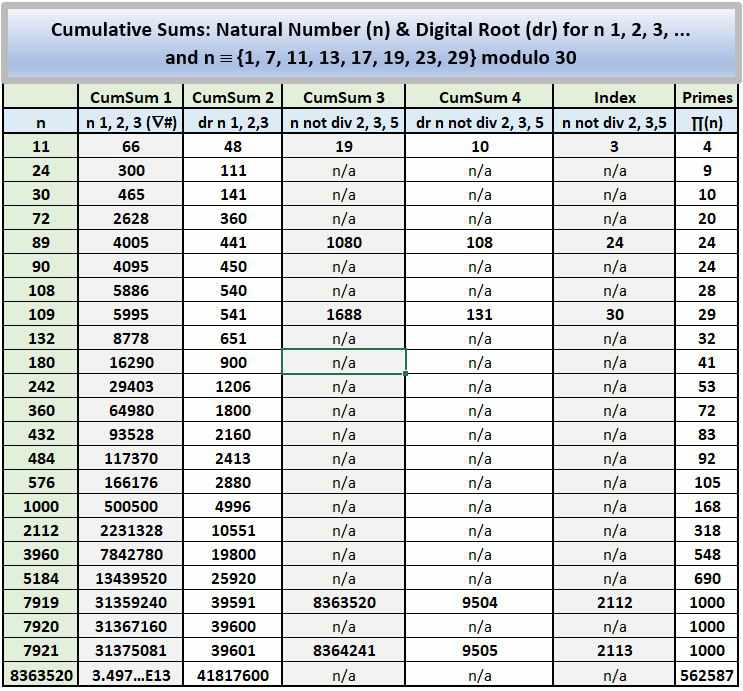
3. Cumulative Sums (k) for n ≌ {1, 7, 11, 13, 17, 19, 23, 29} Modulo 30 (parsed modulo 30)
Referencing the right-hand (pink) column:
Input = n ≌ {1, 7, 11, 13, 17, 19, 23, 29} Modulo 30;
Output (k) = Cumulative Sum (1 → n):

4. Cumulative Digital Root Sums (k) for n ≌ {1, 7, 11, 13, 17, 19, 23, 29} Modulo 30 (parsed modulo 90)

The Two Indexing Fomulae:
1. Input = natural numbers 1, 2, 3, ..., i.e., Index #;
Output = n congruent to {1, 7, 11, 13, 17, 19, 23, 29} Modulo 30.
Parsing by modulo 8 congruence allows us to input index numbers and output the numbers not divisible by 2, 3, or 5 the inputs reference. The 8 negative adjustments per cycle form four bilateral pairs summing to 3.75, and 4 * 3.75 = 15. [Note that the ratio N = {0, 1, 2, 3, ...} to n not divisible by 2, 3, or 5 converges ascendantly to 30/8 = 3.75. For example 89/24 (24 being 89's index number, and thus the ratio's denominator) = 3.708333... while 7919/2112 (2112 = 7919's index number) = 3.7495265151.., etc. Reverse the ratio and the series converges descendently to 8/30 = .2666...].
n ≌ {1} mod 8: k = n * 30/8 − 2.75 = n ≌ {1} mod 30
n ≌ {2} mod 8: k = n * 30/8 − 0.50 = n ≌ {7} mod 30
n ≌ {3} mod 8: k = n * 30/8 − 0.25 = n ≌ {11} mod 30
n ≌ {4} mod 8: k = n * 30/8 − 2.00 = n ≌ {13} mod 30
n ≌ {5} mod 8: k = n * 30/8 − 1.75 = n ≌ {17} mod 30
n ≌ {6} mod 8: k = n * 30/8 − 3.50 = n ≌ {19} mod 30
n ≌ {7} mod 8: k = n * 30/8 − 3.25 = n ≌ {23} mod 30
n ≌ {0} mod 8: k = n * 30/8 − 1.00 = n ≌ {29} mod 30
Here are the first 24 outputs of the stair-stepping formula:
k = 1 * 30/8 − 2.75 = 1
k = 2 * 30/8 − 0.50 = 7
k = 3 * 30/8 − 0.25 = 11
k = 4 * 30/8 − 2.00 = 13
k = 5 * 30/8 − 1.75 = 17
k = 6 * 30/8 − 3.50 = 19
k = 7 * 30/8 − 3.25 = 23
k = 8 * 30/8 − 1.00 = 29
k = 9 * 30/8 − 2.75 = 31
k = 10 * 30/8 − 0.50 = 37
k = 11 * 30/8 − 0.25 = 41
k = 12 * 30/8 − 2.00 = 43
k = 13 * 30/8 − 1.75 = 47
k = 14 * 30/8 − 3.50 = 49
k = 15 * 30/8 − 3.25 = 53
k = 16 * 30/8 − 1.00 = 59
k = 17 * 30/8 − 2.75 = 61
k = 18 * 30/8 − 0.50 = 67
k = 19 * 30/8 − 0.25 = 71
k = 20 * 30/8 − 2.00 = 73
k = 21 * 30/8 − 1.75 = 77
k = 22 * 30/8 − 3.50 = 79
k = 23 * 30/8 − 3.25 = 83
k = 24 * 30/8 − 1.00 = 89
Here's an example using these indexing formulae that exposes a deep connection between the Fibonacci sequence and natural numbers not divisible by 2, 3, or 5. This sequence is interesting regardless of the primality of the indexed numbers, given the beauty of the progression itself.
Fibo digit string ... Fibo string Indexed to N not divisible 2, 3, 5 (primality).
1 ... 1.
11 ... 41 (prime).
112 ... 419 (prime).
1123 ... 4211 (prime).
11235 ... 42131 (prime).
112358 ... 421339 (prime).
11235813 ... 42134297 (prime).
1123581321 ... 4213429951 (composite).
112358132134 ... 421342995499 (composite).
11235813213455 ... 42134299550453 (composite).
1123581321345589 ... 4213429955045957 (composite).
2. Input = n ≌ {1, 7, 11, 13, 17, 19, 23, 29} Modulo 30;
Output = natural numbers 1, 2, 3, ..., i.e., Index # of Input.
For these formulae, reference the left-hand (green) column of the graphic for #3 of the four Cumulative Sum Formulae, above.
Examples:
Here are several examples employing the above formulae. The roles played by these particular numbers in our 'system of thought' have been discussed at various points throughout this site.
We end this section with an interesting way to generate a string of reciprocals for n congruent to {29} modulo 30 employing a few of the above formulae, where:
k = index # for n ≡ {29} modulo 30 as a member of n ≡ {1,7,11,13,17,19,23,29} mod 30 (i.e., n not divisible by 2, 3, or 5).
30/8 = ratio N = {0, 1, 2, 3, ...} to n not divisible by 2, 3, or 5.
k/n x 30/8−1 = 1/n (i.e., n's reciprocal).
Examples; Four primes ≡ {29} mod 30:
8/29 x 30/8−1 = 1/29.
16/59 x 30/8−1 = 1/59.
24/89 x 30/8−1 = 1/89.
2112/7919 x 30/8−1 = 1/7919.
The explanation for this becomes evident when we examine the formula for calculating index # (k) of n ≡ {29} mod 30:
k = (n+1) x 8/30.
Return to www.primesdemystified.com Home Page
Your feedback welcome! Email: gwc@hemiboso.com






