Introduction
It can be proven by a simple process of elimination that all twin prime pairs (p, p+2) greater than (5,7), i.e., starting with (11,13), must have digital root sequencing of either {2,4}, {5,7} or {8,1}. Namely: the digital root of n repeats with period-9, thus {1, 2, 3, 4, 5, 6, 7, 8, 9} {repeat …}. Given twin primes are p, p+2, and given any prime number greater than 3 cannot have digital root of 3, 6, or 9 (leaving digital roots 1, 2, 4, 5, 7, 8) the only possible p, p+2 twin prime dyads are (2,4), (5,7) and (8,1).
That being said, the proof that follows is stronger in that it deterministically contextualizes the digital root sequencing of all twin prime pairs greater than (5,7).
Steps to a Proof
Employing the Prime Spiral Sieve (or a modulo 30 factorization wheel) as an analytical tool, coupled with deductive logic, we will argue a Proof by Construction demonstrating that all twin prime pairs (p, p+2) greater than (5,7), i.e., starting with (11,13), must have digital root sequencing of either {2,4}, {5,7} or {8,1} (the deterministic result of being paired and sequenced as numbers ≌ {11,13}, {17,19} or {29,1} modulo 30).
1. Narrow the field to natural numbers ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30 (oeis.org/A007775). This infinite sequence is commonly known as “natural numbers not divisible by 2, 3 or 5,” and by definition contains all prime numbers > 5 and their multiplicative multiples. And thus it is that prime numbers 2, 3 and 5, and the two pairs of twin primes that 3 and/or 5 populate, (3,5) and (5,7), are excluded from our domain.
2. Populate the Prime Spiral Sieve with the sequence defined in Step 1, where 1 = 12°. Upon doing so, numbers ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30 distribute evenly to 8 radii: {12°, 84°, 132°, 156°, 204°, 228°, 276°, 348°} and when consolidated into a single number line have a repetition cycle of 1{+6+4+2+4+2+4+6+2} {repeat…}. Each of the spiral's 8 radii increments a difference sequence of +30 per rotation: For example, numbers ≌ {1} modulo 30 increment as follows: 1, 31, 61, 91, 121, 151, 181 ... Consequently, every rotation around the modulo 30 wheel increments each of the 8 radii by +3 in digital root terms.
3. Upon completing Step 2, we see that the twin prime candidate field can be further sieved given that — with the exception of (5,7), which we've already excluded by definition from our field of study — numbers radiating at 84° (or numbers ≌ {7} modulo 30) and 276° (or numbers ≌ {23} modulo 30) cannot possibly be twin primes given that their closest possible proximity to prime numbers is +4 and -4, respectively. We have now winnowed the field of twin prime candidates to numbers ≌ {1, 11, 13, 17,19, 29} modulo 30 (oeis.org/A230462), which, when consolidated into a single number line, has a repetition cycle of 11{+2+4+2+10+2+10} {repeat…}, accounts for 6/30 or precisely 20% of natural numbers, and consists of an infinite string of twin prime candidates, (n, n+2), starting with (11,13).
4. As stated in Step 2, the digital roots of the 8 radii increment +3 with each rotation. It follows that the digital root sequences of the 8 radii have a deterministic dependence upon the digital roots of the first 8 elements of the spiral (the 'initializers' in the 8 starting blocks, so to speak) where 1, 7, 11, 13, 17, 19, 23, 29 equate to digital roots 1, 7, 2, 4, 8, 1, 5, 2. The 8 radii thus sequence as follows (and as a side note, we draw your attention to the perfect bilateral 9-sum symmetries):
numbers ≌ {1} mod 30 sequence as {1,4,7} (viz. dr(1+3) = 4; dr(4+3) = 7; dr(7+3) = 1; repeat.)
numbers ≌ {7} mod 30 sequence as {7,1,4}
numbers ≌ {11} mod 30 sequence as {2,5,8}
numbers ≌ {13} mod 30 sequence as {4,7,1}
numbers ≌ {17} mod 30 sequence as {8,2,5}
numbers ≌ {19} mod 30 sequence as {1,4,7}
numbers ≌ {23} mod 30 sequence as {5,8,2}
numbers ≌ {29} mod 30 sequence as {2,5,8}
5. As stated in Step 3, for the purposes of examining twin prime digital root sequencing, we can ignore numbers ≌ {7, 23} modulo 30, leaving us with numbers ≌ {1,11,13,17,19,29} modulo 30, and their corresponding deterministic digital root sequencing:
numbers ≌ {1} mod 30 sequence as {1,4,7}
numbers ≌ {11} mod 30 sequence as {2,5,8}
numbers ≌ {13} mod 30 sequence as {4,7,1}
numbers ≌ {17} mod 30 sequence as {8,2,5}
numbers ≌ {19} mod 30 sequence as {1,4,7}
numbers ≌ {29} mod 30 sequence as {2,5,8}
When we pair these as (n, n+2) dyads (twin prime candidate couplings) we see that:
Numbers ≌ {11,13} mod 30 sequence as:
(11,13) = digital roots {2,4}
(41,43) = digital roots {5,7}
(71,73) = digital roots {8,1}
{digital roots repeat …}
Numbers ≌ {17,19} mod 30 sequence as:
(17,19) = digital roots {8,1}
(47,49) = digital roots {2,4}
(77,79) = digital roots {5,7}
{digital roots repeat …}
Numbers ≌ {29, 1} mod 30 sequence as:
(29,31) = digital roots {2,4}
(59,61) = digital roots {5,7}
(89,91) = digital roots {8,1}
{digital roots repeat …}
Conclusion
We conclude that all twin prime candidates (n, n+2) greater than (5,7) that are potentially twin primes (p, p+2) distribute to one of three digital root dyadic sequences: {2,4} (oeis.org/A232880), {5,7} (oeis.org/A232881) or {8,1} (oeis.org/A232882). □
Appendment (01.11.2015): We can also deduce from the above Construction that all twin prime candidates (n, n+2) greater than (5,7) distribute to one of three modulo 30 dyadic sequences. Namely: they must be paired as numbers ≌ {11,13}, {17,19} or {29,1} modulo 30.
Modulo 90 Configuration Reveals Period-24 Bilateral Sum Symmetry
Given that the digital root of our domain is period-24, when the domain's horizon is framed modulo 90 instead of modulo 30, all digital roots align by numbers ≌ {1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, 79, 83, 89} modulo 90 (note 12 bilateral 90 sums = 1080 = 360 x 3), which equates to the period-24 digital root sequence {1, 7, 2, 4, 8, 1, 5, 2, 4, 1, 5, 7, 2, 4, 8, 5, 7, 4, 8, 1, 5, 7, 2, 8} {repeat ...} (oeis.org/A246508) (possessing 12 bilateral 9 sums = 108). The table below is configured as such, and demonstrates that twin prime candidates, starting with (11,13), sequence as ({2,4}, {8,1}, {2,4}, {5,7}, {2,4}, {5,7}, {8,1}, {5,7}, {8,1}) ({repeat ...}), thus consistent with our proof that an infinity of twin prime candidates n, n+2, starting with (11,13), must have digital root sequencing of either {2,4}, {5,7} or {8,1}. (For emphasis we've color-coded twin prime candidates n, n+2 and twin prime pairs p, p+2.):
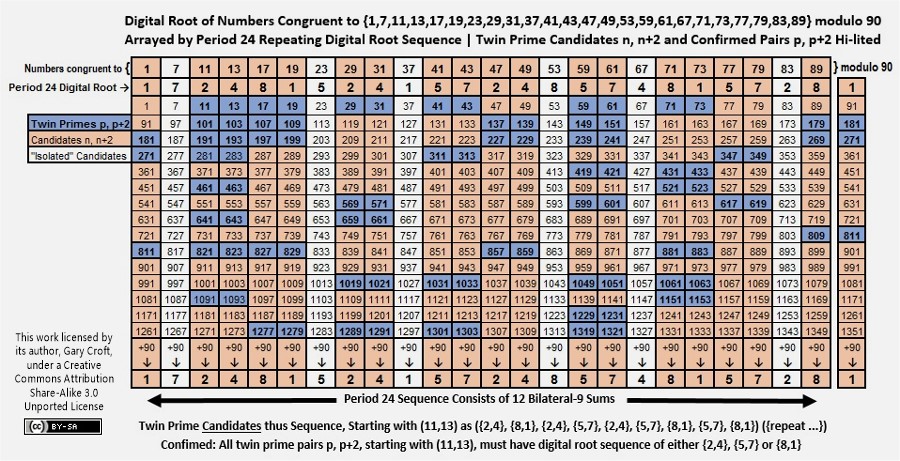
Furthermore, the above modulo 90 matrixing of natural numbers not divisible by 2, 3, or 5, configured to align with its period-24 digital root, forms the basis for a proof that:
digital root {2,4} = n ≌ { (11,13), (29,31), (47,49) } mod 90
digital root {5,7} = n ≌ { (41,43), (59,61), (77,79) } mod 90
digital root {8,1} = n ≌ { (17,19), (71,73), (89,1) } mod 90
And it follows that for all twin primes > (5,7):
digital root {2} = n ≌ {11, 29, 47} mod 90
digital root {4} = n ≌ {13, 31, 49} mod 90
digital root {5} = n ≌ {41, 59, 77} mod 90
digital root {7} = n ≌ {43, 61, 79} mod 90
digital root {8} = n ≌ {17, 71, 89} mod 90
digital root {1} = n ≌ { 1, 19, 73} mod 90
Return to Twin Primes Demystified | Return to Primes Demystified Home Page
Your feedback welcome! Email: gwc@hemiboso.com