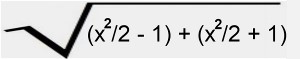Twin Primes: Hidden Dimensions and Symmetries
The factorization algorithms in tandem with rotating symmetry groups that ultimately determine the distribution of twin primes (p, p+2 or 'prime numbers with a gap of two') are fascinating to behold. Below we demonstrate how the Prime Spiral Sieve generates these symmetries in the form of algorithmically permutated mapping matrices, palindromes, rotating equilateral triangles, and complex polygons. The latter include {9/3} star polygons and the beautiful 'palindromagon,' the construction of which sequences the six possible permutations of {3,6,9} palindromically; namely:
639→693→963←369←396←936
[Note: If you're thinking this is 'sacred geometry,' you'd be mistaken. While many will find these symmetries transcendently beautiful, they are nonetheless humbly rooted in elementary modular and digit sum arithmetic augmented with the most basic geometry. Numinousness is in the eye of the beholder.]
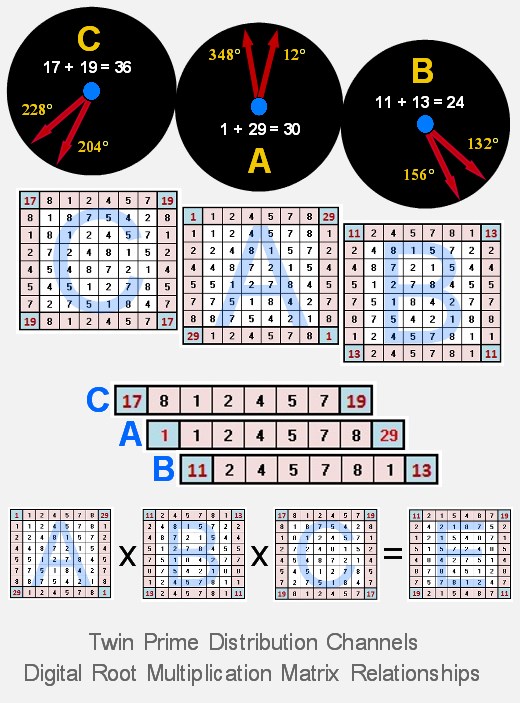
Twin Prime Distribution Channels
We begin our exploration of twin primes by spiraling numbers congruent to {1, 7, 11, 13, 17, 19, 23, 29} modulo 30 (otherwise defined as natural numbers not divisible by 2, 3 or 5) within a modulo 30 factorization wheel (see graphic, below), where 1 = 12°. By definition this sequence consists of the number one (1) and all prime numbers greater than 5 and their multiplicative multiples, the latter starting with 7 x 7 = 49, the first composite number in our factorization domain. (Ref: https://oeis.org/A007775)
Spiraling the sequence in Archimedean intervals of 30 in this way exposes the fact that all twin prime candidates (n, n+2), and confirmed twin prime pairs (p, p+2) greater than (5,7) parse along three distinct "distribution channels," i.e., starting with (11,13) potential twin primes are separated by 24° and parsed equally along three sets of paired radii: {348° ↔ 12° } ... {132° ↔ 156°} ... {204° ↔ 228°}:
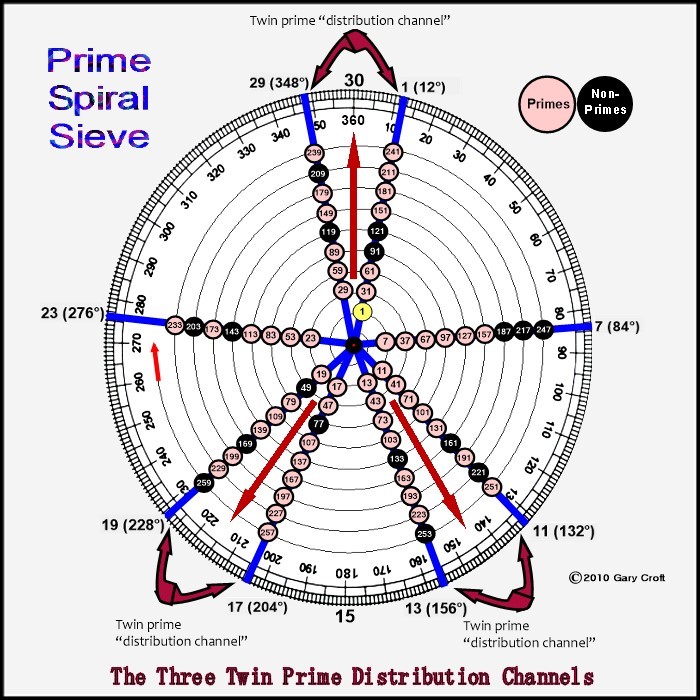
[Note: If you're unfamiliar with modular arithmetic and congruence relations, another way of expressing n ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30 would be to define it as: Natural numbers with remainders {1, 7, 11, 13, 17, 19, 23, or 29} when divided by 30. For example, 37, 67, and 97 all have remainders of 7 when divided by 30, and therefore we'd say that 97 ≌ ('is congruent to') {7} modulo 30.]
Below we translate the three twin prime distribution channels into the language of modular and digit sum arithmetic and express them as simple functions. To account for composite numbers within our domain, we then explore the beautiful clockworks of modulo 90 factorization. The clock starts ticking with the cycling of 242 = 576 digital root dyads in period-24 sequences tri-leveled to form 3 x 3 matrices. These in turn rotate vertices {1,4,7}, {2,5,8}, {3,6,9} of the equilateral triangles within {9/3} star polygons.
Also indicated are the digital roots of the (n, n+2) dyad sums, which – for reasons we demonstrate below – must be either 3, 6 or 9, while the digital root of their n(n+2) products must be 8 in all three cases.
[Note: On this site digital root (also known as repeated digit sum, iterated sum-of-digits, or modulus 9 function) refers to the single digit (1-9) that results when all digit sums are summed in turn, e.g., 47 = 4+7 = 11 = 1+1 = 2; and thus the digital root of 47 = 2, or dr(47) = 2. This in turn reflects the fact that any natural number is congruent modulo 9 to its digital root, i.e., when you divide a whole number by 9, the remainder is the number's digital root.]
Numbers ≌ {11,13} modulo 30 (at 132° & 156°) sequence as:
(11,13) = digital roots {2,4} → 2 + 4 = digital root 6
(41,43) = digital roots {5,7} → 5 + 7 = digital root 3
(71,73) = digital roots {8,1} → 8 + 1 = digital root 9
{digital roots repeat...}
Numbers ≌ {17,19} modulo 30 (at 204° & 228°) sequence as:
(17,19) = digital roots {8,1} → 8 + 1 = digital root 9
(47,49) = digital roots {2,4} → 2 + 4 = digital root 6
(77,79) = digital roots {5,7} → 5 + 7 = digital root 3
{digital roots repeat...}
Numbers ≌ {29, 1} modulo 30 (at 348° & 12°) sequence as:
(29,31) = digital roots {2,4} → 2 + 4 = digital root 6
(59,61) = digital roots {5,7} → 5 + 7 = digital root 3
(89,91) = digital roots {8,1} → 8 + 1 = digital root 9
{digital roots repeat...}
All of the n, n+2 twin prime candidates listed above sequence their digital roots in one of three variations: {2,4}, {5,7} or {8,1}. We prove why this is so for all twin prime pairs (11,13) or greater in our Proof by Construction for the Digital Root Sequencing of Twin Primes. This Proof simultaneously demonstrates that all twin prime candidates (n, n+2) greater than (5,7) distribute to one of three modulo 30 dyadic sequences, i.e., numbers ≌ to {11,13}, {17,19} or {29,1} modulo 30.
We've documented the three twin prime digital root dyad sequences on the On-Line Encyclopedia of Integer Sequences (and we explore the beautiful symmetries they generate at great length down this page). Here are the OEIS sequence numbers and links:
A232880: Twin primes with digital root 2 or 4
A232881: Twin primes with digital root 5 or 7
A232882: Twin primes with digital root 8 or 1
In our 'Foundations' section, we stated that the 'set of natural numbers not divisible by 2, 3 or 5' is equivalent to:
n ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30.
Factor sieving this set leaves all primes > 5, including all twin primes greater than (5,7). Sub-sorting (to use a spreadsheet term) the prime pair candidates in the twin prime distribution channels can be expressed as:
n ≌ {1, 11, 13, 17, 19, 29} modulo 30;
with the additive sum sequence:
1{+10+2+4+2+10+2} {repeat ...}.
This narrows the factor-sieving field from 8/30 to 6/30, or exactly 20% of natural numbers. We've documented this sequence on the On-Line Encyclopedia of Integer Sequences oeis.org Sequence Number A230462.
Digital Root Sieving, Modulo 90
"It was through my search for meaning that I discovered how important the digital root space is, which in return rewarded me with a look at how elegant and beautiful the world really is." – Talal Ghannam, Ph.D., The Mystery of Numbers Revealed Through Their Digital Root
Framing our factorization domain (natural numbers not divisible by 2, 3, or 5) in modulo 90 rather than modulo 30 terms expands the number of twin prime distribution channels from 3 to 9, as pictured here:
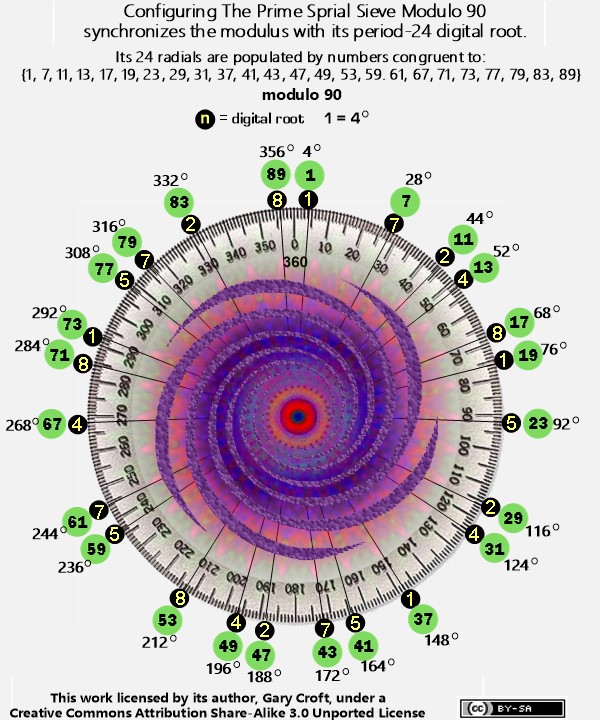
The advantage of telescoping our frame of reference to modulo 90 is that it synchronizes the modulus with its period-24 digital root and thus parses twin prime candidates by their digital root dyads {2,4}, {5,7} and {8,1}, as follows:
digital root {2,4} = n ≌ { (11,13), (29,31), (47,49) } mod 90: 11{+2+16+2+16+2+52} {repeat ...}
digital root {5,7} = n ≌ { (41,43), (59,61), (77,79) } mod 90: 41{+2+16+2+16+2+52} {repeat ...}
digital root {8,1} = n ≌ { (17,19), (71,73), (89, 1) } mod 90: 17{+2+52+2+16+2+16} {repeat ...}
Further disaggregating the sieving action, it follows that for all twin primes > (5,7):
digital root {2} = n ≌ {11, 29, 47} mod 90: 11{+18+18+54} {repeat ...}
digital root {4} = n ≌ {13, 31, 49} mod 90: 13{+18+18+54} {repeat ...}
digital root {5} = n ≌ {41, 59, 77} mod 90: 41{+18+18+54} {repeat ...}
digital root {7} = n ≌ {43, 61, 79} mod 90: 43{+18+18+54} {repeat ...}
digital root {8} = n ≌ {17, 71, 89} mod 90: 17{+54+18+18} {repeat ...}
digital root {1} = n ≌ {19, 73, 1} mod 90: 19{+54+18+18} {repeat ...}
Sorting the digital root congruence sets sequentially reveals perfect diagonal and central-vertical 90-sum symmetry (color-coded in the graphic below):

The matrix below makes these congruence relationships clear:
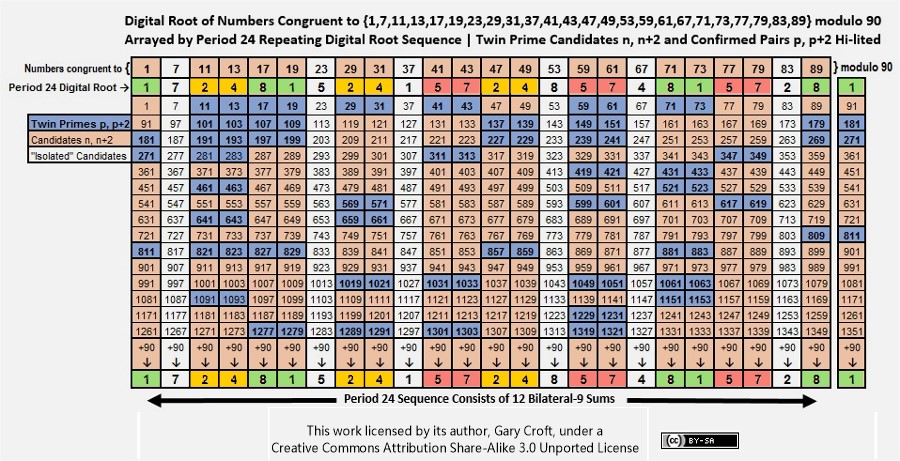
This matrix also reveals that the digital root sequencing of the twin prime candidate dyads (starting with 11, 13) is period-18:
{2 4, 8 1, 2 4, 5 7, 2 4, 5 7, 8 1, 5 7, 8 1} {repeat ...}.
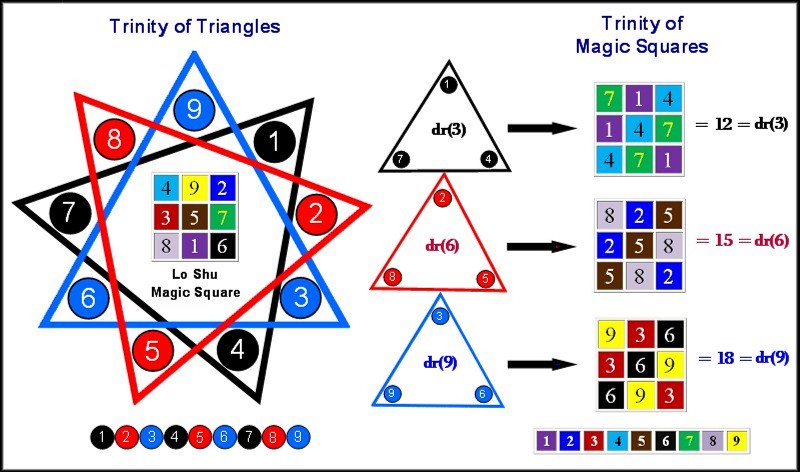
The Trinity of Rotating Equilateral Triangles
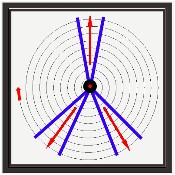
Earlier we drew your attention to the fact that the sums of the twin prime digital root dyads must equal 3, 6 or 9. We did so because these represent a triad, {3,6,9}, which – with {1,4,7} and {2,5,8} – are the vertices of rotating equilateral triangles that taken together constitute the "Trinity of Triangles" (illustrated below).
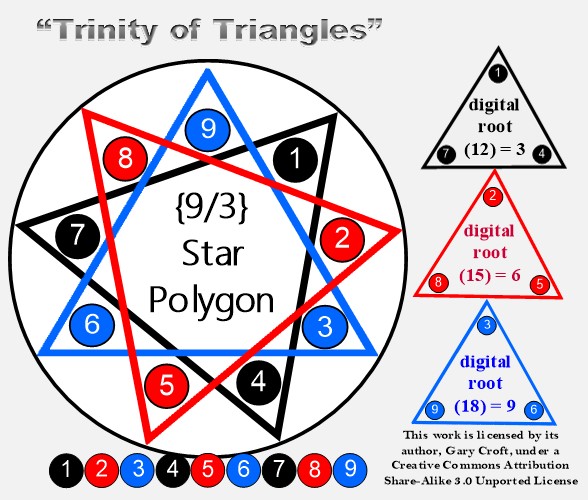
Below we will demonstrate how factorization algorithms and twin prime dyad cycling at the digital root level rotate the vertices of equilateral triangles within {9/3} star polygons like the one pictured above. These rotations are encoded in 3 x 3 matrices generated by period-24 digital root dyad tri-level cycling. We will also reveal the Latin Square reflecting {3,6,9} hidden in plain sight betwixt and between the twin prime distribution channels; all of its rows, columns and principal diagonals summing to 18.
Consolidation of the Twin Prime Distribution Channels
Consolidating the 6 radii used to construct the three twin prime distribution channels into a single number line completely isolates twin prime candidates, pairing them in tandem in a deterministic sequence, starting with (11, 13), thus:
1 {+10+2+4+2+10+2} {repeat ... ∞}.
Noting that the first term in the sequence is 1 + 10 = 11, we find, for example, that six of the first seven such pairings are twin primes (and we should add that all twin primes within this range are accounted for):
(11, 13) (17, 19) (29, 31) (41, 43) (47, 49 = 7x7) (59, 61) (71, 73) ...
(Excluded by definition are numbers ≌ {7, 23} mod 30, sequencing as 7 {+16+14} {repeat ... ∞}. With the exception of 7, members of this sequence cannot form twin prime pairs given their closest possible proximity to neighboring prime numbers is +4 and -4, respectively.)
Below is a matrix showing the distribution of twin prime sets (both candidates and confirmed prime pairs) from (11, 13) to (569, 571):

The first three twin prime sets in this matrix configuration are an anagram, in angular terms (in a 30-sectioned circle such as encompasses the Prime Spiral Sieve, where 1 = 12°), to the first three primes, thus: (11, 13) (17, 19) and (29, 31) respectively translate to:
11 + 13 = 24 ... 24° = 2
17 + 19 = 36 ... 36° = 3
29 + 31 = 60 ... 60° = 5
[You'll note that the sum of the intervals for each row of twin prime candidates = 2 x 3 x 5 = 30, and that the intervals separating the first 36 twin prime pair candidates sum to 360, i.e., between (11, 13) and (359, 361), bringing the candidate sets full circle, so to speak; and interestingly the product of the sums of the first three twin prime candidate sets = 24 x 36 x 60 = 51840, while 51840/192 = 270; 51840/360 = 122; 51840/432 = 120; and 51840/576 = 90. Why these particular divisions are interesting will become clear later down this page.]
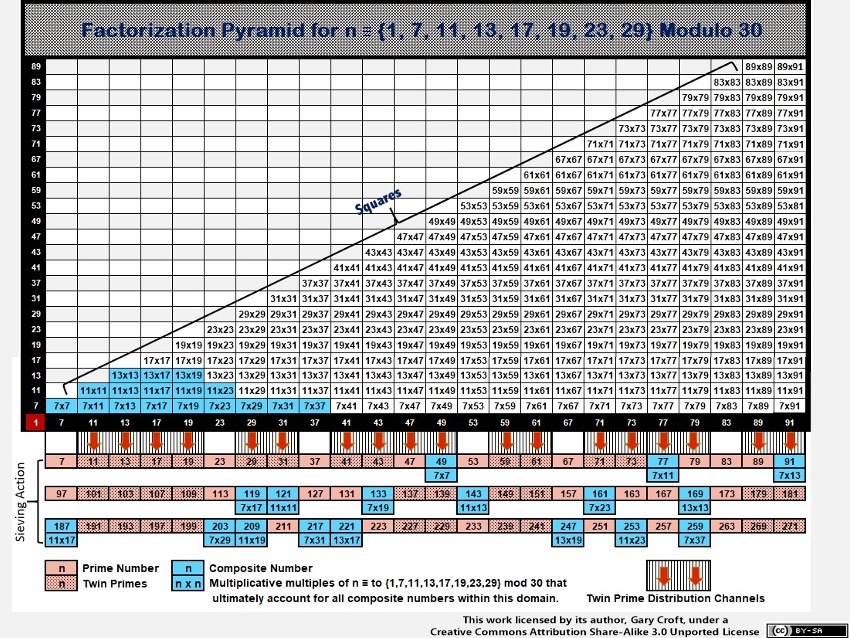
Factorization Algorithms for the Twin Prime Candidates
All composite numbers in the twin prime distribution channels can be accounted for algorithmically by the eight-fold modulo 30 progressions shown below where we factor-sieve by division then multiplication.
[Note: The algorithms shown here are a sub-set of the
chordal progressions discussed at some length earlier that factored all composite numbers in the array populated by natural numbers not divisible by 2, 3 or 5, as opposed to only factoring those impacting twin prime candidates, demonstrated below.]
The matrix that follows shows factorization by sequential division specific to the twin prime distribution channels. The left-most column consists of the number 1 (which we've dubbed 'silent') and members of the twin prime distribution channels in sequence, thus delimiting the prospective factorization to twin prime candidates.
Essentially, we've sequentially divided numbers ≌ {1, 11, 13, 17, 19, 29} mod 30 by numbers ≌ {1, 7, 11, 13, 17, 19, 23, 29} mod 30. All modulo n ≌ 0 (i.e., zero remainder) results generated (except when a number is divided by itself) indicate factors (arrayed horizontally, hi-lited in pink) of composite numbers n (arrayed vertically, also hi-lited in pink), while twin primes are hi-lited in bright blue and primes not belonging to a twin prime pair are hi-lited in yellow.
When the square root of any number in the twin prime distribution sequence is reached without producing a remainder of zero, the number must by definition be prime. For example, the square root of 311 is 17.6352... When 311 is divided in turn by 7, 11, 13, and 17 no zero remainders are produced (and, regardless, for obvious reasons 17 can't possibly be one of 311's factors). The next possible factorization within our defined domain, 192 = 361, is out of range, and therefore 311 must be prime. Here's the division factorization algorithm matrix:
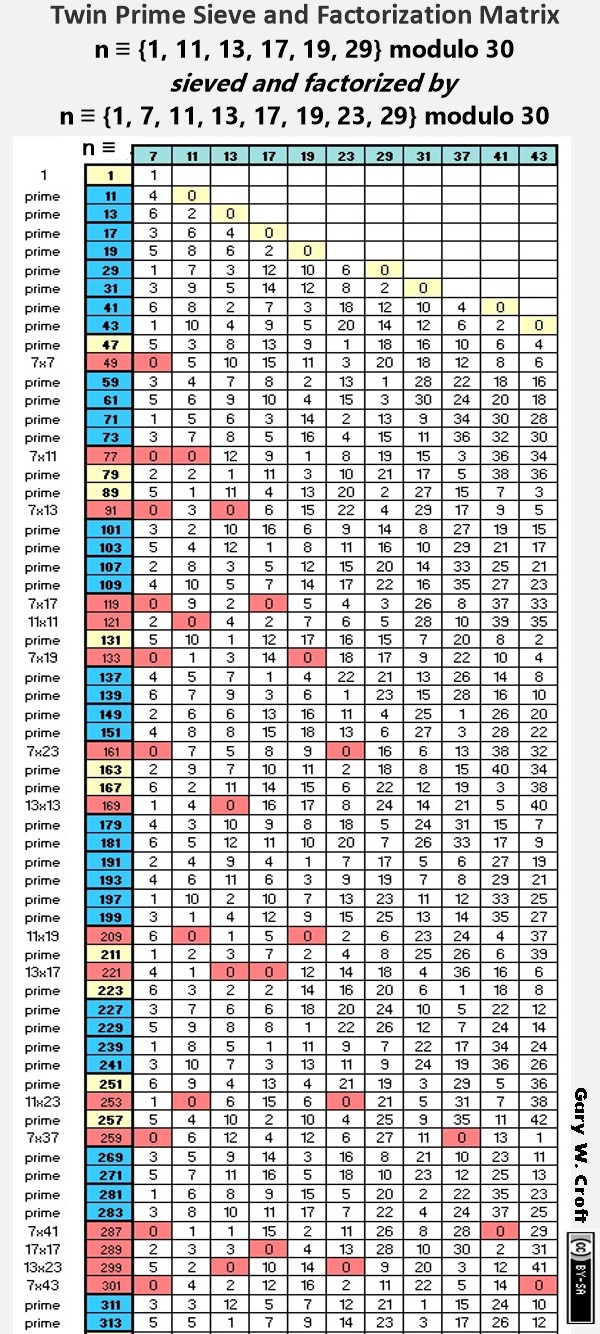
Below we show only the calculations required to determine primality of twin prime candidates within the designated range of 11 to 313. This illustrates the significant increase in sieving efficiency that results from the fact that you need only activate divisors when their squares are reached. For example, you needn't begin dividing by 11 until its square, 121, is reached. And of course, from a programmer's perspective, the sieve has another built-in efficiency in that division into a given twin prime candidate stops immediately upon encountering a remainder of zero (0) identifying it as composite:

Multiplicative factorization sequencing (illustrated in the graphic below) is simply a reversal of the division process shown above. This algorithm is self-evidently more efficient than it's division sibling given every 'beat' indexes (identifies) a composite number (Although we should caution, as we detail under
Counting Primes, some composite numbers get 'hit' more than once. These redundant factorizations do put a measure of drag on efficiency.). Given that in this case we're illustrating the sequencing in a modulo 90 frame, those factorizations impacting twin primes are n ≌ {1, 11, 13, 17, 19, 29, 31, 41, 43, 47, 49, 59, 61, 71, 73, 77, 79, 89} modulo 90 (initiated by 7 * 7= 49, as 1 is 'silent'). From this, it shouldn't be surprising to learn that the density of prime numbers as a percentage of real numbers graphs roughly at a 45° angle–a mirror image of the factorization geometry, which we can think of as a graphic representation of factorization density.
Twin Prime Distribution Channel Functions
The three twin prime distribution channels can be defined as functions, where:
x = natural numbers 1, 2, 3, ...
f(x) = 30x -19, -17 ... gives n ≌ {11,13] mod 30
f(x) = 30x -13, -11 ... gives n ≌ {17,19} mod 30
f(x) = 30x -1, +1 ... gives n ≌ {29,1} mod 30.
Below we delineate the functions with examples (the first two twin prime candidate dyads generated by each):

Beautiful Palindromagon Constructed from Twin Prime Digital Root Dyad Cycles
"The concept of symmetry is simple, elegant and intuitive... Symmetry is not just frivolous window dressing to a theory, but in fact is an essential feature that indicates some deep underlying physical principle." – Michio Kaku, The God Equation
And now to pull the proverbial rabbit out of the hat. On our page devoted to factorization we demonstrate that when sequenced vertically and grouped in sets of three pairs, the period-24 digital root dyad cycles generated by the Prime Spiral Sieve's factorization algorithms produce permutating equilateral triangles in the form of 3 x 3 matrices from which can be extrapolated the vertices of {9/3} star polygons. As a reminder, here's one of the graphics we used on our factorization page to illustrate these operations. Here we focus on vertice rotations for numbers congruent to {7} modulo 90:
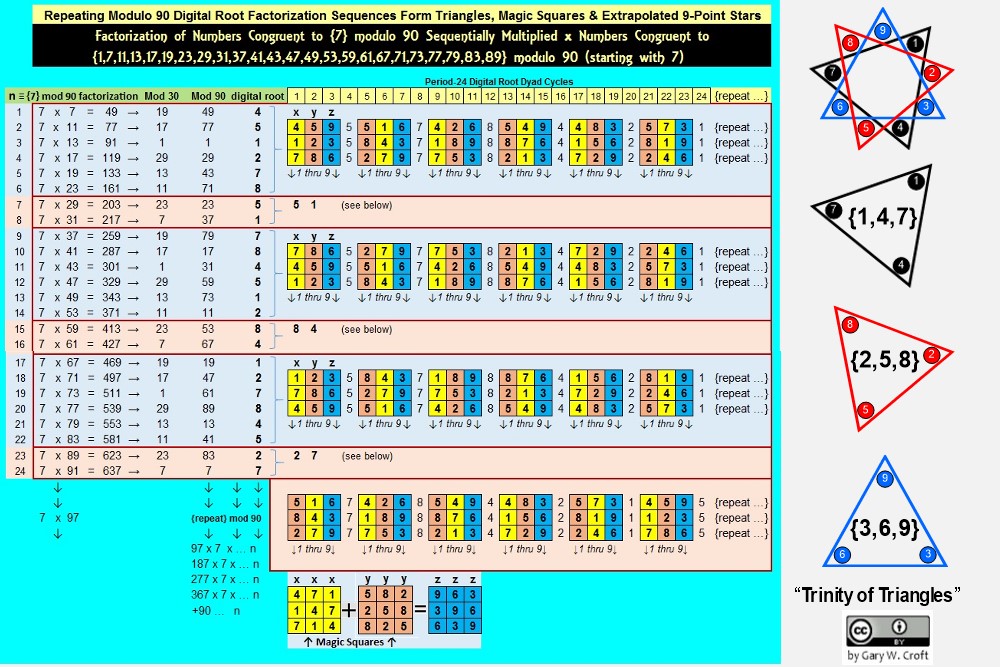
An obvious question: What happens when the generator cycles are sequenced horizontally? The answer, it turns out, is pleasing to both mind and eye.
For discussion sake, we'll focus on twin primes. They, like the factorization algorithms discussed above, are permutated via 3 x 3 matrices populated by numbers 1 thru 9 and initiated (generated) by a trio of dyads involving digital roots 1, 2, 4, 5, 7, 8, which–when sequenced algorithmically–combinatorially form elegant 'geo-arithmetric' symmetry groups.
Elsewhere on this site we published a "Proof by Construction for the Digital Root Sequencing of Twin Primes" demonstrating that all twin prime pairs greater than (5,7), i.e., starting with (11,13) must have digital root sequencing of either {2,4}, {5,7} or {8,1}. A perfect example of such cascading dyads would be the first three prime twinnings of numbers congruent to {11,13} modulo 30: {11,13 = digital root 2 + 4 = 6} + 30 {41,43 = digital root 5 + 7 = 3} + 30 {71,73 = digital root 8 + 1 = 9} ...
When we additively sum the three period-24 digital root cycles these dyads produce, then tier them, we create six 3 x 3 matrices (each containing values 1 thru 9) separated by repetitive number tiers in the following order: {1,1,1} {5,5,5} {7,7,7} {8,8,8} {4,4,4} {2,2,2}. The six matrices these tiers demarcate are the source of triangular coordinates when translated into vertices of a modulo 9 circle (which by definition has 9 equidistant points around its circumference, each separated by 40°).
The series of diagrams below show the six geometric stages culminating in a complex polygon of extraordinary beauty. We've dubbed this object a 'palindromagon' given that the coordinates of the 18 triangulations produced by the digital root dyadic cycles in the order sequenced sum to a palindrome: 639 693 963 369 396 936. Remarkably, this periodic palindrome, with additive sum of 108, sequences the 6 possible permutations of values {3,6,9}. Interesting to consider a geometric object with a hidden palindromic dimension. But that's not all: When the six triadic permutations forming the palindrome are labeled A, B, C, D, E, F in the order generated, ACE and BDF form 3 x 3 Latin squares. In both cases all rows, columns and principal diagonals sum to 18:
ACE ... BDF
693 ... 639
369 ... 963
936 ... 396
The output of these algorithmically sequenced triangulations is fundamentally a geometric representation of the twin prime distribution channels (and, as we noted above, the same geometry is expressed in factorization sequencing, albeit the vertices may be ordered differently. This is because each set of three generator dyads roots to the same six elements: 1, 2, 4, 5, 7, 8. Thus, for example, dyad sets ({1,2} {4,5} {7,8}) and ({2,4} {5,7} {8,1}) will generate identical complex polygons, despite their vertices being sequenced in different orders.).
It's remarkable that objects consisting of star polygons, spiraling irregular pentagons, and possessing nonagon perimeters and centers, can be constructed from only 27 coordinates pointing to 9 triangles in 3 variations. Each period-24 cycle produces two 'palindromagons,' as illustrated below:
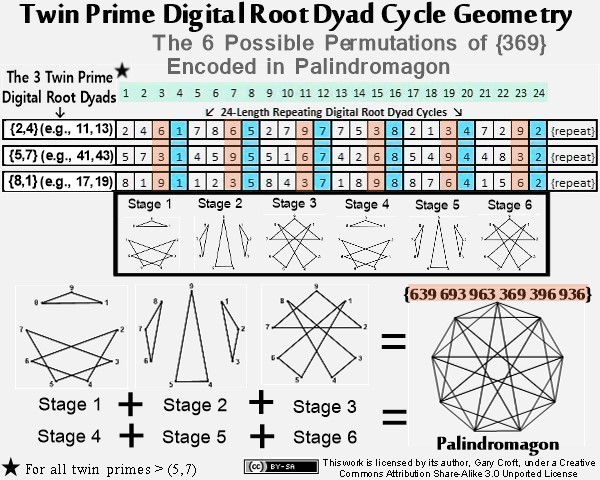
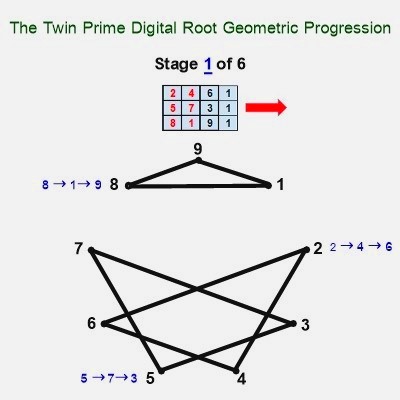
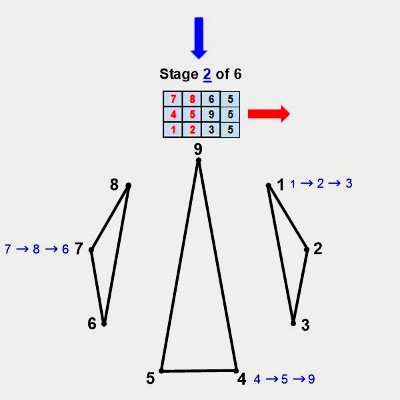
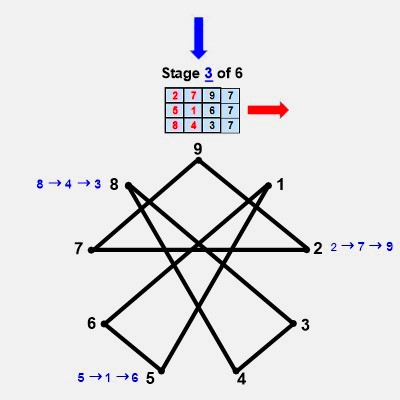
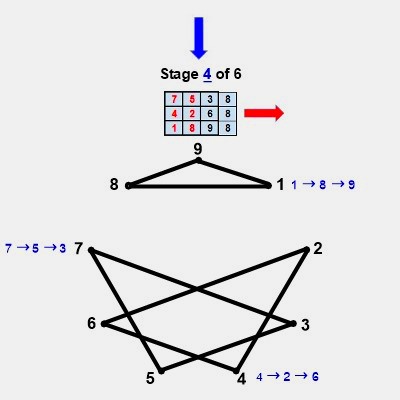
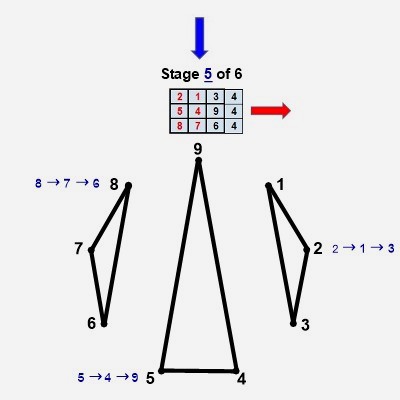
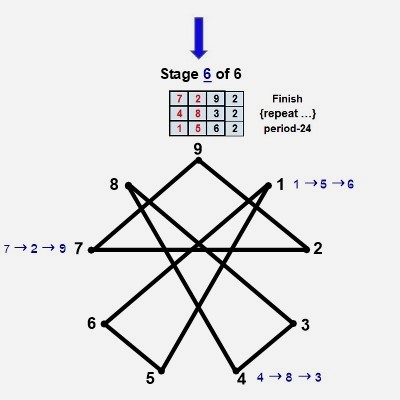
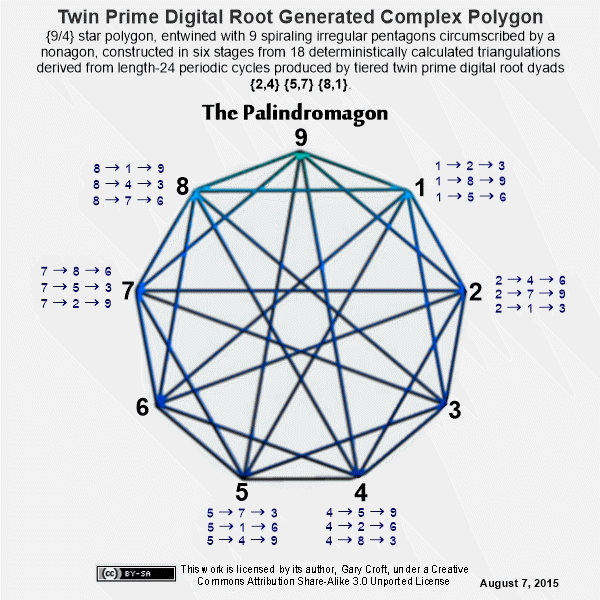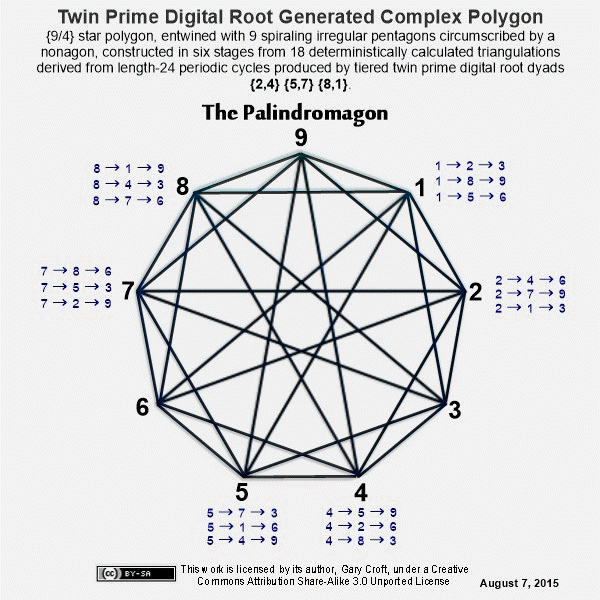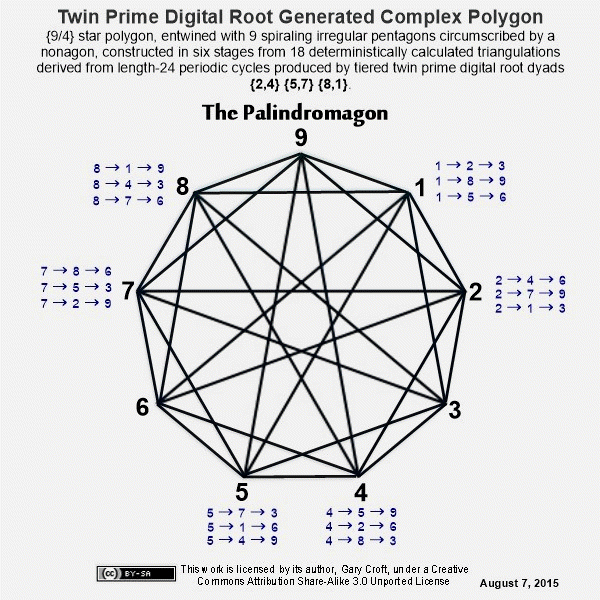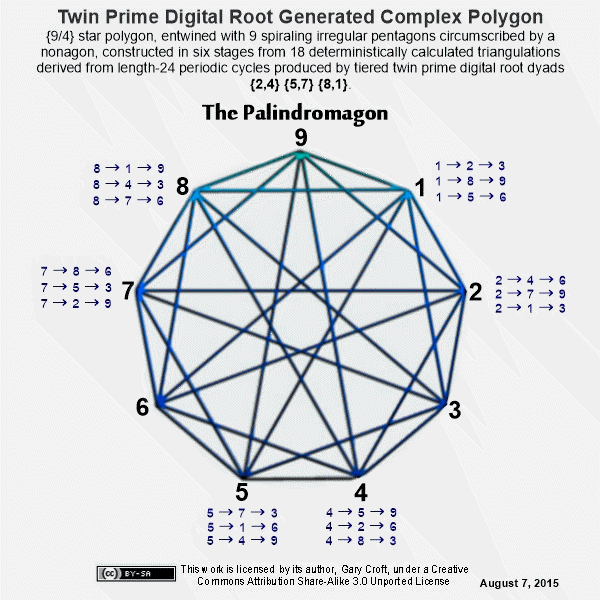
The only vertices not directly connected by edges in the palindromagon are {1,4,7}, {2,5,8}, and {3,6,9}, i.e., a {9/3} star polygon is powerfully present by virtue of its distinct absence. This is 'rectified' when we next combine the vertical triangulations from our digital root cycles forming {9/3} star polygons with the horizontally generated Palindromagon, and discover that the consolidated object is one well known to geometers: It's a Regular enneazetton (8-simplex) (or a 9-faceted polytope in 8 dimensions), which, according to Wikipedia, contains: 9 vertices, 36 edges, 84 triangle faces, 126 tetrahedron cells, 126 5-cell 4-faces, 84 5-simplex 5-faces, 36 6-simplex 6-faces, and 9 7-simplex 7-faces. And from graph theory we learn that, given every vertex is connected to every other vertex, the enneazetton is defined as a 'complete graph.'
In sum, we're positing that Palindromagon + {9/3} Star Polygon = Regular Enneazetton (pictured below). The significance of this 'chain-of-events' is that we can state with deterministic certainty that cycling the period-24 digital root dyads of both twin primes and the modulo 90 factorization sequences of numbers not divisible by 2, 3, or 5 generates an infinite progression of these complex polygons possessing stunning reflectional and translational symmetries.
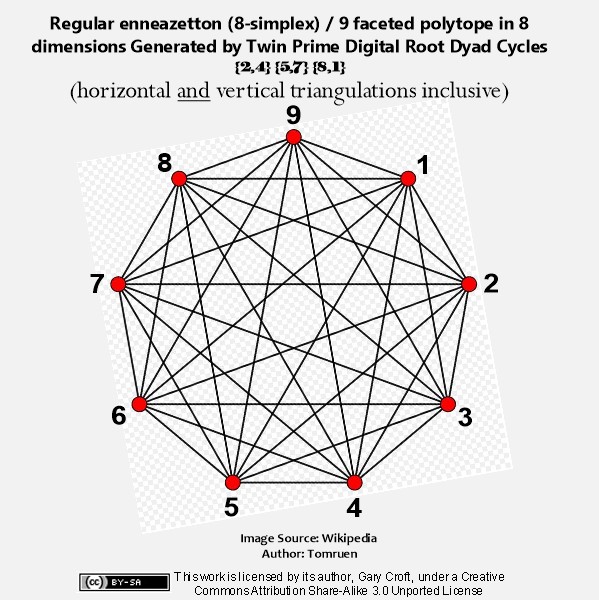
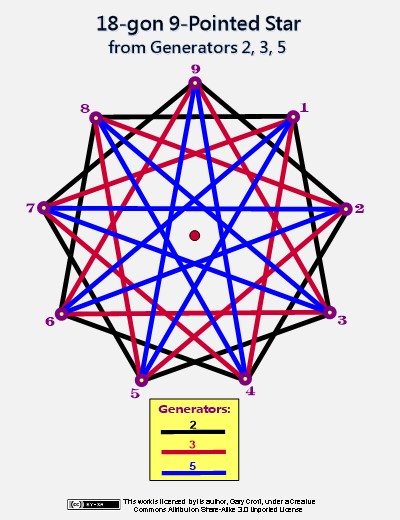
Lastly, let's compare the above-pictured 'enneazetton' to an 18-gon 9-point star generated by the first three primes; 2, 3 and 5 (pictured below), and we see that they are identical, save for the number of sides (9 vs. 18). They are essentially convex and concave versions of each other. This is geometric confirmation of the deep if not profound connection between the three twin prime distribution channels (which remember have 2, 3, and 5 encoded in their Prime Spiral Sieve angles) and the first three primes, 2, 3, and 5:
Additive Compilation of the Twin Prime Candidates
From what we learned above about segregating twin prime candidates, we can demonstrate that they compile additively in perfect progression, completing an infinite sequence of circles (multiples of 30 and 360):
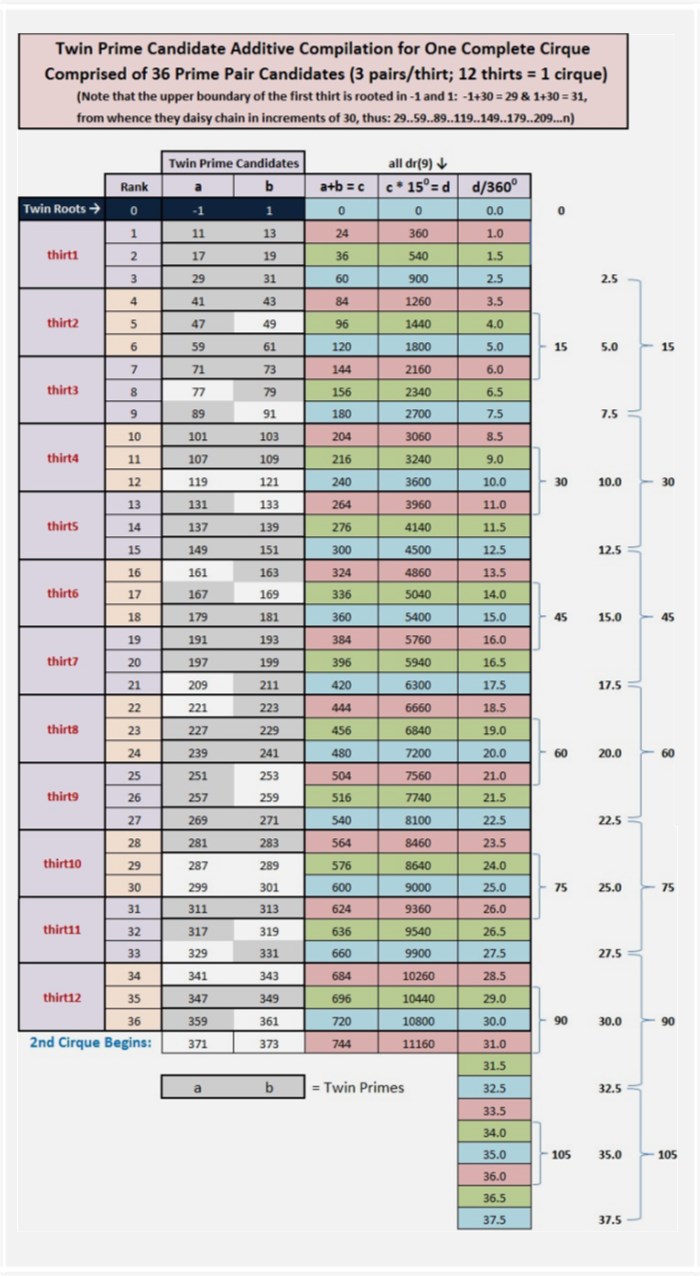
We've multiplied the twin prime candidate pair sums by 15° to show the equivalent arc of rotation of each pair in a modulo 90/24-element per rotation spiral, where 1 = 15° and 24 x 15 = 360°. Thus, when you divide the products by 360°, you get circular equivalents, e.g., 11+13=24; 24x15=360; 360/360=1 (thus, the 1st pair in the first thirt is equivalent to one 360° rotation).
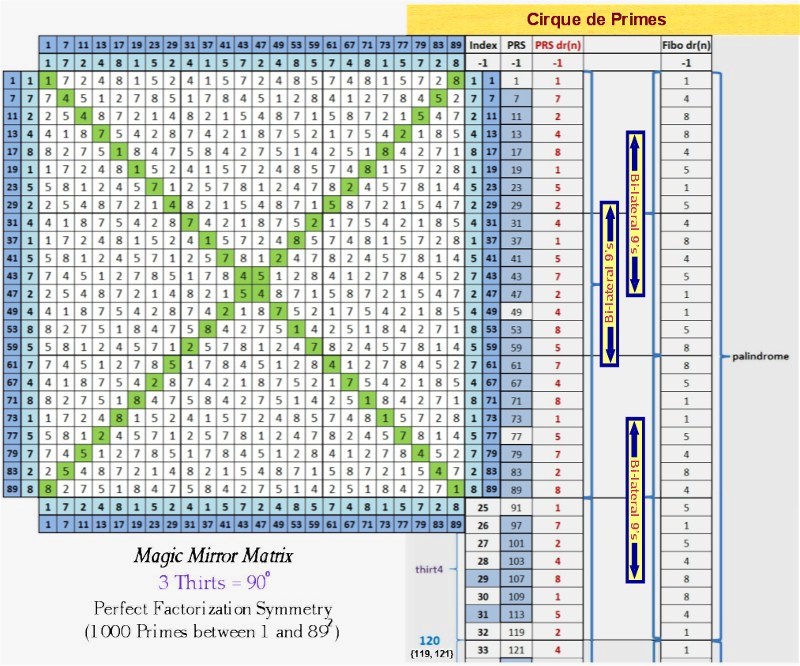
Cirque de Primes
A thirt, in case you're wondering, is a useful unit of measure when discussing intervals in natural numbers not divisible by 2, 3 or 5. A thirt, equivalent to one rotation around the Prime Spiral Sieve is like a mile marker on the prime number highway. If we take the Modulo 30 Prime Spiral Sieve and expand it to Modulo 360, we see that there are 12 thirts in one complete circle, or 'cirque' as we've dubbed it. Each thirt consists of 8 elements. The first two thirts are {1,7,11,13,17,19,23,29} and {31,37,41,43,47,49,53,59}. The last element in thirt1, 29, and the 1st element in thirt2, 31, are rooted in -1 and 1, respectively: where -1+30=29 and 1+30=31. These are twin primes, followed by an infinite sequence in intervals of 30 of twin prime candidates, that serve as the center stripes of the prime number highway, and thus: {-1,+1} +30 {29,31} +30 {59,61} +30 {89,91} +30 {119,121} +30 {149,151} +30 {179,181} +30 {209,211} +30 {239,241} +30 {269,271} +30 {299,301} +30 {329,331} +30 {359,361} completes cirque1, albeit, paradoxically, 361 is the start of cirque2. You can say that {359,361} straddle the 1st and 2nd cirques exactly at 360°, just as {719,721} straddle cirque2 and cirque3 at 720 (or 360x2) ... This is congruent with the fact that all repeating patterns at the digital root level, including the digital roots of Fibonnaci numbers and Lucas numbers indexed by our domain as well as the digital roots of the set constituting our domain, achieve in toto end-to-end symmetrical resolution at 360° intervals, which, of course, is aesthetically satisfying.
Here's a graphic that illustrates these relationships:
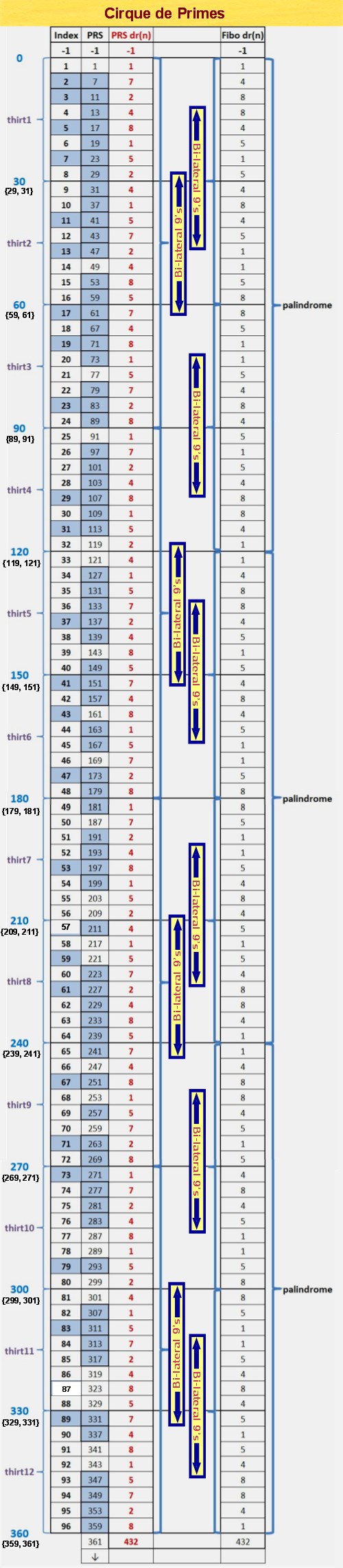
All prime numbers among the index numbers and the Prime Root Set have been hi-lited in blue. Of the 24 index numbers that are prime, 22 point to elements of the Prime Root Set that are also prime; and the two that aren't, 161 (7x23) & 221 (13x17), are both semi-primes with factors that sum to 30 (and, interestingly, the 30th index # points to 109, a prime number that–like 89–has a decimal expansion based on the Fibonnaci sequence). Also note that 1092 - 892 = 3960 = 11*360.
We see from the graphic above that the digital roots of the Fibonacci numbers indexed to our domain (Numbers ≌ to {1,7,11,13,17,19,23,29} modulo 30) repeat palindromically every 32 digits (or 4 thirts) consisting of 16 pairs of bilateral 9 sums. The digital root sequence of our domain, on the other hand, repeats every 24 digits (or 3 thirts) and possesses 12 pairs of bilateral 9 sums. The entire Prime Root sequence end-to-end covering 360° has 48 pairs of bilateral 9 sums. And finally, the Prime Root elements themselves within the Cirque, consisting of 96 elements, has 48 pairs of bilateral sums totaling 360. Essentially, the prime number highway consists of infinitely telescoping circles ... Also note, the digital roots of the Prime Root Set as well as the digital roots of Fibonnaci numbers and Lucas numbers (the latter not shown above) indexed to it all sum to 432 (48x9) in 360° cycles. The sequence involving Fibonacci digital roots repeats every 120°, and has been documented by the author on the On-Line Encyclopedia of Integer Sequences: Digital root of Fibonacci numbers indexed by natural numbers not divisible by 2, 3 or 5 (A227896). (As an aside, we believe the genesis of the Fibonacci sequence is deepened when rooted in -1,1 rather than 1,1, thus creating identity symmetry: -1,1,0,1,1,2,3,5,8 ... Reverse the first two terms (-1 & 1) to generate negative Fibonacci series: 1,-1,0,-1,-1,-2,-3,-5,-8 ...)
[Note: In some circles (no pun intended) the number 432 (as in 432 Hertz) has been declared the "frequency of the cosmos" to which the "Music of the Spheres" is tuned. A growing number of musicians and musicologists support tuning musical instruments to A=432Hz (or Pythagorean A) rather than the standard concert pitch of A=440Hz. They claim that 432Hz, with its 12-scale octave overtones compared to 440Hz's 8 octaves, is harmonically richer and cleaner in sound (The author, who plays American World Music on a flamenco guitar, will attest to this.). It's clear, upon analyzing the cirque de primes, that the digital roots sum to 432 in 360° cycles encompassing 12 thirts. Common sense, if not mathematical rigor, would suggest that there is some correspondence to 432hz's 12-scale octave overtones (and in fact, the Prime Spiral Sieve is featured prominently on this Latin American website's page titled "Fundamental Theorem of Arithmetic Applied Musically to the Zodiacal Circle"). Go to YouTube.com, search on "432," and you'll be impressed by the number of videos featuring this number.]
Cirque de Primes Juxtaposed with the Magic Mirror Matrix
Now lets zoom in to examine the first 90° partition (encompassing 3 thirts) of our Cirque de Primes, that starts with 1 and ends with 89. By juxtapositioning the 'Magic Mirror Matrix' against this range (see graphic, below), beautiful hidden symmetries are revealed at the digital root level when matrix factorized. This symmetry repeats every 90 degrees, repeatedly incrementing all 24 elements +90 (jumping from 1 thru 89 to 91 thru 179 then +90...n) while the digital roots never change. And thus, this 'geoarithmetric' object, telescoping to infinity, represents the factorization sequencing that accounts for all composite numbers extant in the set of natural numbers not divisible by 2, 3 or 5, leaving all prime numbers greater than 5. For an in depth discussion of the 'Magic Mirror Matrix,' including stunning facts about the number 89 (which, among other things, has the Fibonnaci sequence embedded in the decimal expansion of its reciprocal), click here:
Magic Mirror Matrix.
Digital Root Parsing of the Twin Primes
Parsing Twin Primes by their digital roots (in context with natural numbers not divisible by 2, 3 or 5) reveals extremely
interesting patterns. Study the matrix below, and you'll discover that it's a beautiful construct of perfectly balanced, multi-directional,
'logic tight' symmetries:
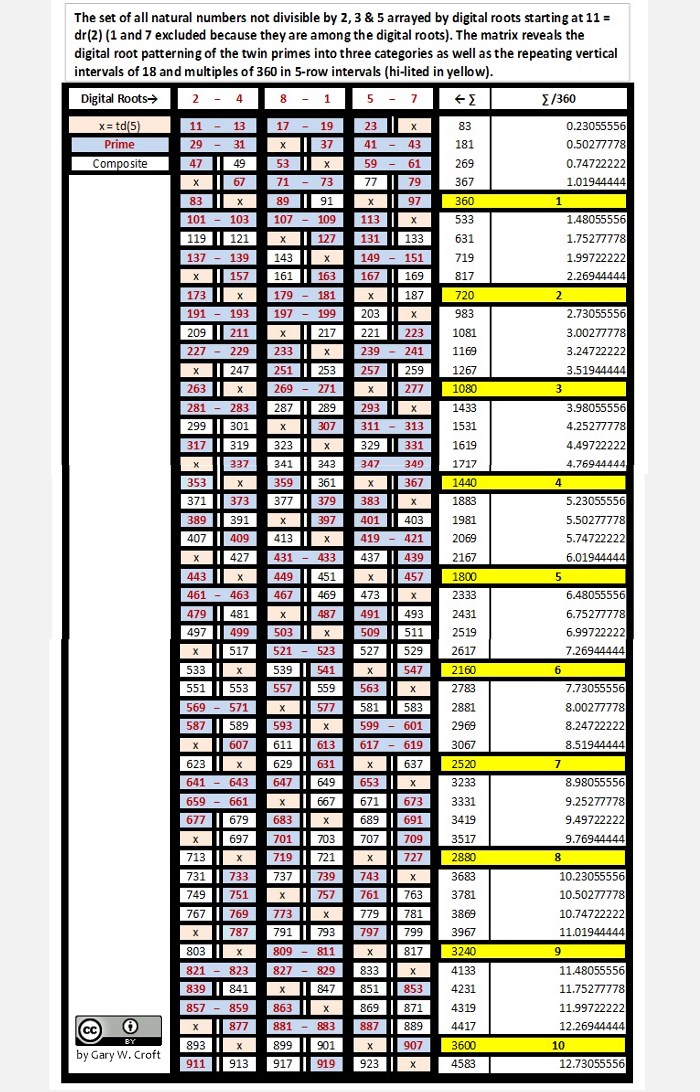
Note 1: As indicated, the pink squares marked with x's denote elements with terminating digits = td(5) (their values neither shown nor added into the row sums, above). Although they are not members of our defined set, they are nonetheless interesting. For one thing,
the first six td(5) elements sum to 360, as follows: 25 + 35 + 55 + 65 + 85 + 95 = 360. For another, they are always adjacent to modulo 30 "Isolated Primes," discussed below.
Note 2: The first six Isolated Primes, starting with 23, also compile to 360, as follows: 23 + 37 + 53 + 67 + 83 + 97 = 360.
Note 3: Seven is the only number arrayed along the two Isolated Prime radii that isn't 'isolated,' given it is twinned with number 5. Were we to include 7 in our summing of isolated primes, above, the result would be 367, which is itself prime and the sum of seven prime numbers.
Note 4: The first 12 elements that are not td(5), consisting of 11 consecutive prime numbers plus 72, also sum to 360, as follows: 11 + 13 + 17 + 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47 + 49 = 360.
Note 5: Every row possesses "sum symmetry" involving three identical sums. The first row, for example, gives us three sums (working outside-in) totaling 36: 11 + 25; 13 + 23; and 17 + 19 = 36 (and given 36 is 360/10, it comes as no surprise that the 10th row has three sums totaling 360). The 2nd row has three sums totaling 72; the 3rd row has three sums totaling 108, etc. Each successive row thus increments +36, and the row sums accumulate in overlapping cycles of 360 and 432 (the curious relationship between these two numbers discussed elsewhere on this site).
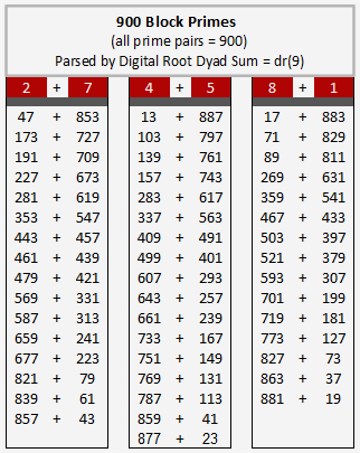
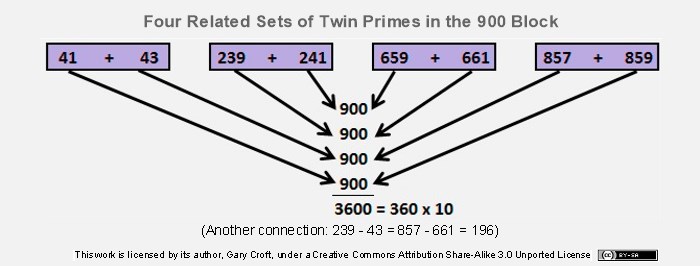
The 900 Block
When we described the Digital Root Parsing Matrix above as 'logic tight,' we were not overstating it. This is evidenced by the
fact that, when elements with a terminating digit of 5 are included, every element in the first 49 rows of the matrix can be coupled with (added to) another element in the matrix to total 900 (with the paired elements spatially located in "equal and opposite" positions). Obviously, each pair totaling 900 must be comprised of elements producing digital root sums that decompose to dr(9). We've dubbed the 48 dyads consisting of two prime numbers totaling 900 in this block '900 Block Primes' (listed below).
[Note: Please keep in mind that it is completely arbitrary of us to fucus on the '900 Block' given there are an infinite number of blocks in an infinite number of incremented configurations within the bounds of the infinitely expandable matrix (e.g., from 47 in Row 3 to 313 in Row 17 forms a '360 Block' and 11 in Row 1 to 1789 in Row 99 (not shown above) would create an '1800 Block').]
The Digital Root Parsing Matrix is structured such that any rectangular configuration with 'n' number of
columns and 'n' number of rows will produce lateral dyadic sum symmetry, determined by the three dr(9) sum variations: {2,7}, {4,5} and {8,1}
(Note: To calculate the bilateral sums for a row, multiply the row's index number times 36.). Here are two examples involving complete (6-element)
rows: Take the 17 rows from 2 thru 18 and you'll produce 51 combinations summing to 360; or take the 5 rows from 19 thru 23, which produces 15
combinations summing to 756 (To calculate the number of combinations for any and all rectangles configured from complete rows, multiply
the given number of rows times 3.). Now lets carve out a rectangle that doesn't utilize complete rows: we create a 4-column/6-row rectangle with
the four corners = 11, 19, 101 and 109 (all prime), and find that all cross-lateral sums equal 120.
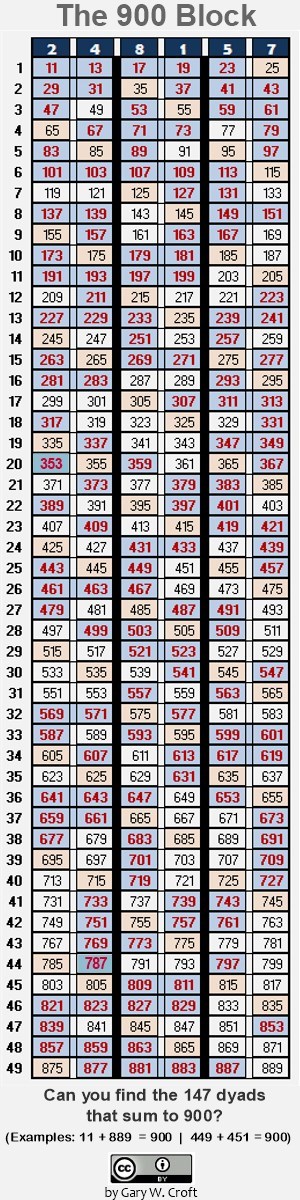
What does this object tell us about twin primes? First, we see that twin primes fall into three categories when parsed by their digital roots: {2,4}, {8,1} and {5,7} (2x4, 8x1 and 5x7 all equal dr(8), while 2+4=dr(6); 8+1=dr(9) and 5+7=dr(3): the three legs of the {3,6,9}
triangulation which is a member of the Trinity of Triangles, discussed toward the bottom of this page. Next we learn that every
twin prime candidate set wihin the '900 Block' has a twin prime candidate pair 'in opposition' creating two sums of 900. Of those falling into this
category within the block above, our favorite consists of four sets of twin primes, thus:
Parsing Digital Root Factorization Dyads
As we demonstrated above, employing the logic of digit sum arithmetic, there are a finite number of factorization combinations that correlate
to each of the six digital roots, for a total of 6 x 6 = 36 dyads.
The diagram below shows the first 26 twin prime candidates (13 pairs) from the Digital Root Parsing Matrix including the
6 composite numbers falling within this range (from {11,13} to {131,133}). For each composite number we show both its digital root and natural factors.
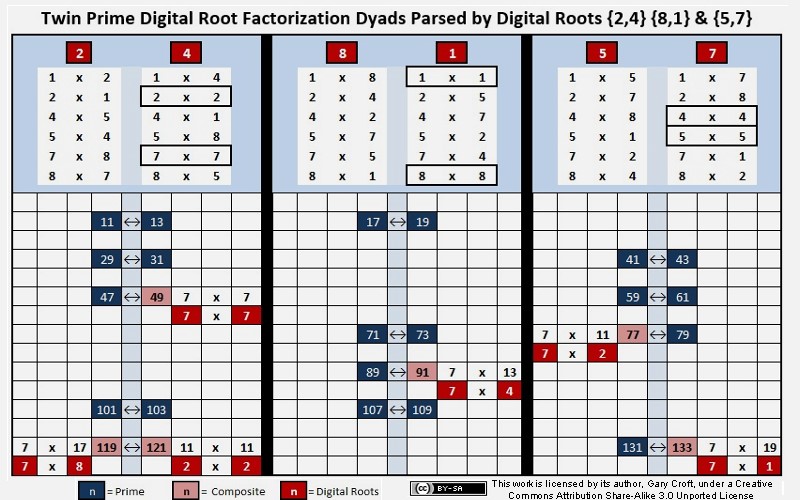
Examining the six digital root dyad factorization groups shown above, we discover that the six sets of multiplicands in every case consist of the triangles {1,4,7} and {2,5,8} (and their rotating variations) interlineated, as we show below ({1,4,7} triangles are in bold to help delineate them):
Digital Root Product = 2: {2, 1, 5, 4, 8, 7}
Digital Root Product = 4: {4, 2, 1, 8, 7, 5}
Digital Root Product = 8: {8, 4, 2, 7, 5, 1}
Digital Root Product = 1: {1, 5, 7, 2, 4, 8}
Digital Root Product = 5: {5, 7, 8, 1, 2, 4}
Digital Root Product = 7: {7, 8, 4, 5, 1, 2}
When the matrix of digital root products is interpreted as a numerical block, we see that all rows and columns sum to 27, and working from the outside in (both vertically and horizontally) we find perfect symmetry involving bilateral 9 sums. This digital root factorization object displays the six possible rotational variations for both {1,4,7} and {2,5,8} triangulations and–speaking of symmetry–does so palindromically. Thus:
{1,4,7}, {4,1,7}, {4,7,1}, {1,7,4}, {7,1,4}, {7,4,1} ... ← palindrome
{2,5,8}, {2,8,5}, {8,2,5}, {5,2,8}, {5,8,2}, {8,5,2} ... ← palindrome
Stringing together the six digital root multiplicand sets produces this beautiful 36-digit palindrome:
215487421875842751157248578124784512.
The significance of these triangles, as members of rotational symmetry groups that can be configured to create a triad of magic squares, is discussed at length toward the bottom of this page.
As we've discussed previously, every pair of twin prime candidates has one element each from the {1,4,7} and {2,5,8} alternating triangulations (and as indicated, all squares distribute to {1,4,7}–never to {2,5,8}).
Most notably, perhaps, digital root parsing reveals the clustering of twin prime candidates into "six packs," i.e., groupings into
three prospective prime pairs demarcated by the isolated prime radii. [Note: The only twin prime set in our domain not in a six-pack {17, 19}
sums to 36, which, as 1/10th of 360, seems poetic. If we were to decrement {17, 19} in two -18 steps, the result would be
17 + 19 - 1 + 1 - 17 - 19 = 0, which makes logical sense (from zero to 180 being consistent with the set incrementation, shown below).] The first
eleven six packs follow (and you'll find the first three of these in the graphic above). And as we alluded, the sets sequence in +180 increments, thus:
11+13 + 29+31 + 47+49 = 180
41+43 + 59+61 + 77+79 = 360
71+73 + 89+91 + 107+109 = 540
101+103 + 119+121 + 137+139 = 720
131+133 + 149+151 + 167+169 = 900
161+163 + 179+181 + 197+199 = 1080
191+193 + 209+211 + 227+229 = 1260
221+223 + 239+241 + 257+259 = 1440
251+253 + 269+271 + 287+289 = 1620
281+283 + 299+301 + 317+319 = 1800
311+313 + 329+331 + 347+349 = 1980
Framing the above as an 11-row/6-column matrix (excluding the row totals), reveals that its 66 elements
form 33 dyads that sum to 360 (e.g, 11+349 = 360). Each column stair-steps in increments of 30 and each row, working from the outside
in, has three identical sums (e.g., the first row has three dyads that sum to 60 each). Also, we find that the repeating digital root
sequences reflect the Trinity of Triangles {3,6,9} {1,4,7} {2,5,8}:
2+4+2+4+2+4: dr(2) + dr(4) = dr(6)
5+7+5+7+5+7: dr(5) + dr(7) = dr(3)
8+1+8+1+8+1: dr(8) + dr(1) = dr(9).
Pointing our discussion of twin prime candidate sequencing triangles back to the Prime Spiral Sieve, we see that three rotations around the Sieve produce six twin prime candidate-related digital root triangles:
11 (2), 13 (4) ... 17 (8), 19 (1) ... 29 (2), 31 (4)
41 (5), 43 (7) ... 47 (2), 49 (4) ... 59 (5), 61 (7)
71 (8), 73 (1) ... 77 (5), 79 (7) ... 89 (8), 91 (1)
Twin Prime Domino Theory
Switching metaphors, below we represent our repeating 'six-pack' clusters as dominoes. The first row of dominoes reveals
patterns shared by all three of the 3-pair twin prime candidate configurations, namely the terminating digit and modulo 30 values array
identically across the three dyads parsed by digital roots. The second row of dominoes reveals the repeating patterns by digital
root and then by digital root with the terminating digit values excluded. [Note: Every category below possesses 'equal and opposite'
sum symmetry. For example, the modulo 30 configuration has 9 lateral sums of 30 each.]

It is evident studying the above that the difference sequence between elements in like positions in the 3-pair clusters is 90.
We know from digit sum arithmetic that when you increment +90, both the original elements and the +90 incremented sums will possess
the same terminating digits, digital roots, n(modulo 30) results, as well as the same digital roots when terminating digit values are
excluded. For example, take the twin prime candidate pairs {89, 91} +90 = {179, 181}:
89: dr(8); td(9); 29(mod 30); dr(n-td) = 8
89+90 = 179
179: dr(8); td(9); 29(mod 30); dr(n-td) = 8
91: dr(1); td(1); 1(mod 30); dr(n-td) = 9
91+90 = 181
181: dr(1); td(1); 1(mod 30); dr(n-td) = 9
The dominoes also tell us that:
The lower-valued (left-hand) member of a prime pair will always possess one of three terminating digit ↔ modulo 30 combinations:
td(1) ↔ 11(mod 30)
td(9) ↔ 29(mod 30)
td(7) ↔ 17(mod 30)
The higher-valued (right-hand) member of a prime pair will always possess one of three terminating digit ↔ modulo 30 combinations:
td(3) ↔ 13(mod 30)
td(1) ↔ 1(mod 30)
td(9) ↔ 19(mod 30)
And lastly, twin prime sets that are: n ≌ 29(mod 30) + 2 = n ≌ 1(mod 30) decompose to: dr(n-td) = 2, 3, 5, 6, 8 or 9,
while all other twin primes sets [namely n ≌ 11(mod 30) + 2 = n ≌ 13(mod 30) and n ≌ 17(mod 30) + 2 = n ≌ 19(mod 30)] decompose to: dr(n-td) = 1, 4 or 7.
The Six Digital Root Multiplication Matrices
When we convert the Twin Prime Distribution Channels and/or the paired radii whose angles sum to 360° into digital root
multiplication matrices, the results are interesting–to say the least. At the digital root level there are six interrelated
matrices of special interest to us: three represent the twin prime distribution channels; the fourth captures the two 'isolated'
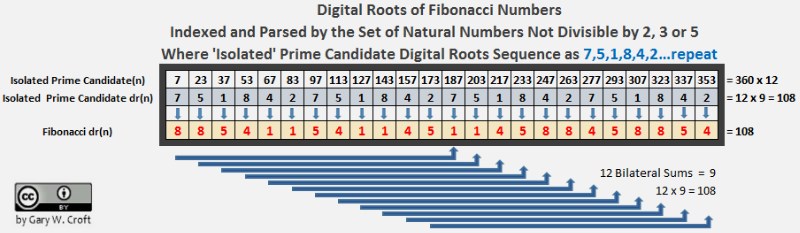
radii of the Prime Spiral Sieve, i.e. where n ≌ 7 (modulo 30), at 84°, and n ≌ 23 (modulo 30), at 276°
(isolated, because, with the exception of 7, which is twinned with 5, the closest proximity they can be to other primes is plus
or minus 4, and therefore they can never be twin primes); the fifth and sixth matrices complete the set of four derived from radii
whose angles = 360° and in modulo 30 terms sum to 30.
Here's a diagram showing the derivation of the six matrices:
img src="Origin_Digital_Root_Matrices.jpg" height="789" width="475" alt="Diagram showing origin of the six digital root matrices"/>
Each of the six matrices draws 24 elements from the first 96 elements of our domain (starting with 1 and ending with 359;
you'll find a deep analysis of these 96 elements under the heading 'Cirque de Primes,' above ...).
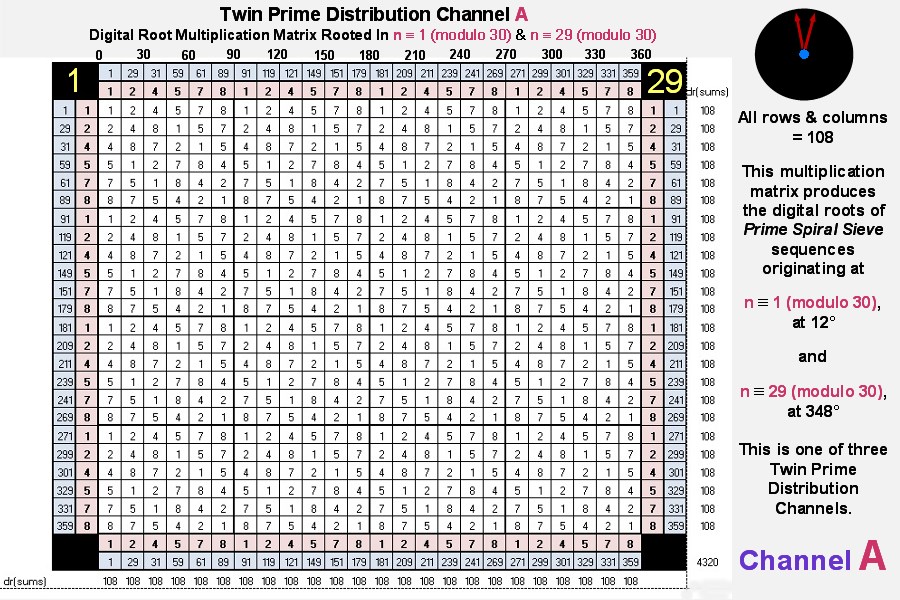
When matrix multiplied, each sequence produces sixteen identical 36-element squares comprised of six 6-element sequences. The matrix derived from
the twin prime distribution channel where n ≌ 1 (modulo 30), at 12°, and n ≌ 29 (modulo 30), at 348°, is pictured
directly below. It has sequences identical to those generated when you take a digital root multiplication matrix (aka Vedic Square) and
remove all 3's, 6's and 9's (This "Imaginary Square," as we dubbed it, is discussed in more detail under
prime factorization).
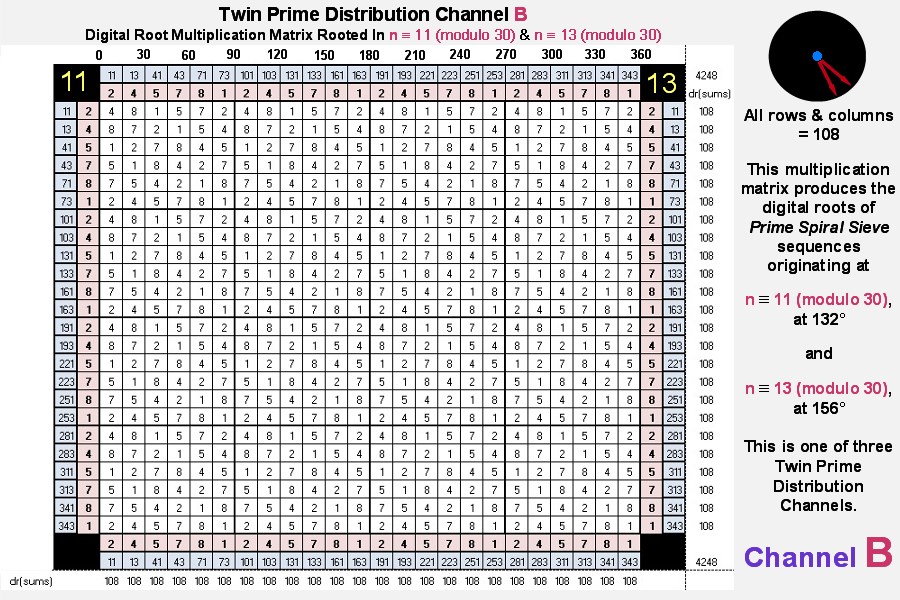
The matrices for twin prime distribution channels B & C follow:
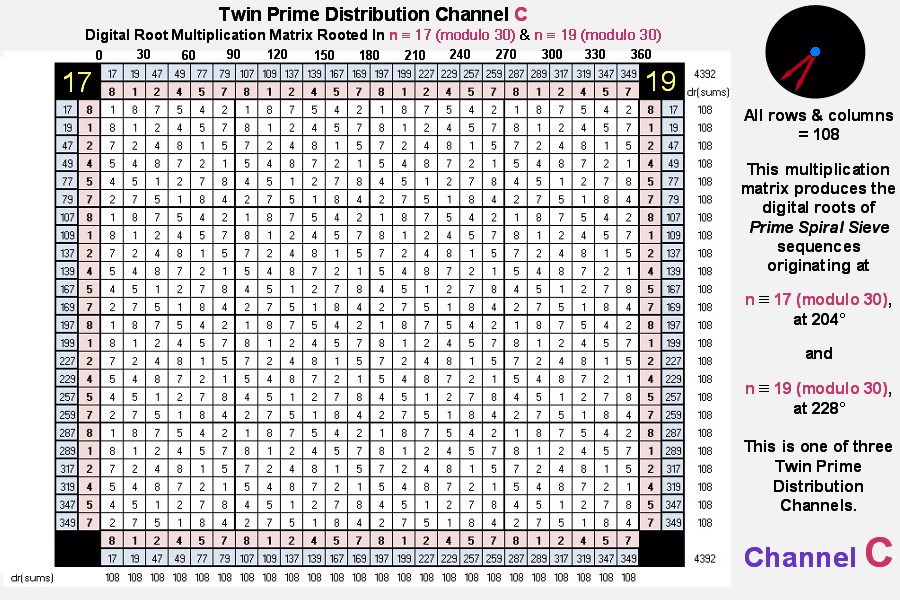
Our next matrix is derived from the Isolated Prime Distribution Radii:
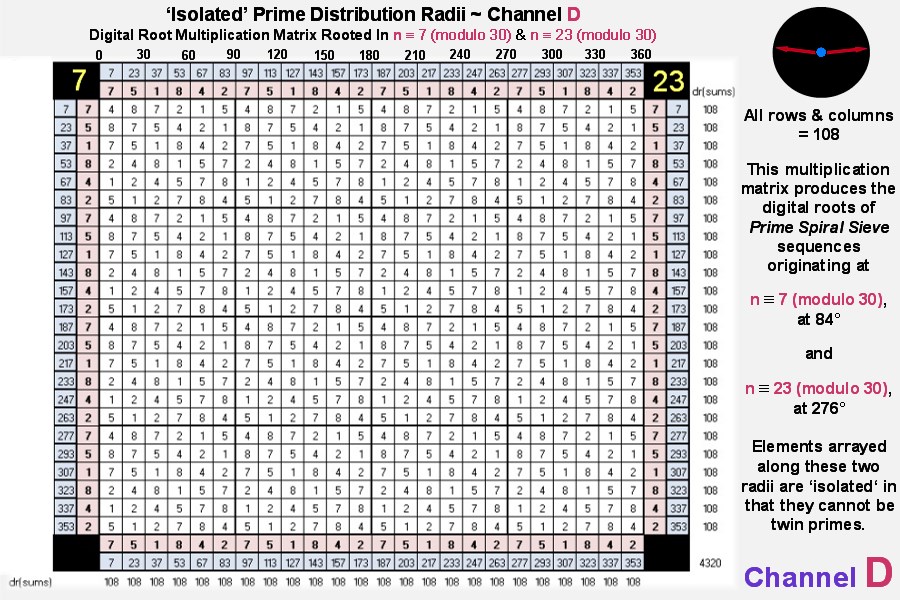
And lastly we present the third and fourth matrices derived from paired diagonals whose angles sum to 360°:
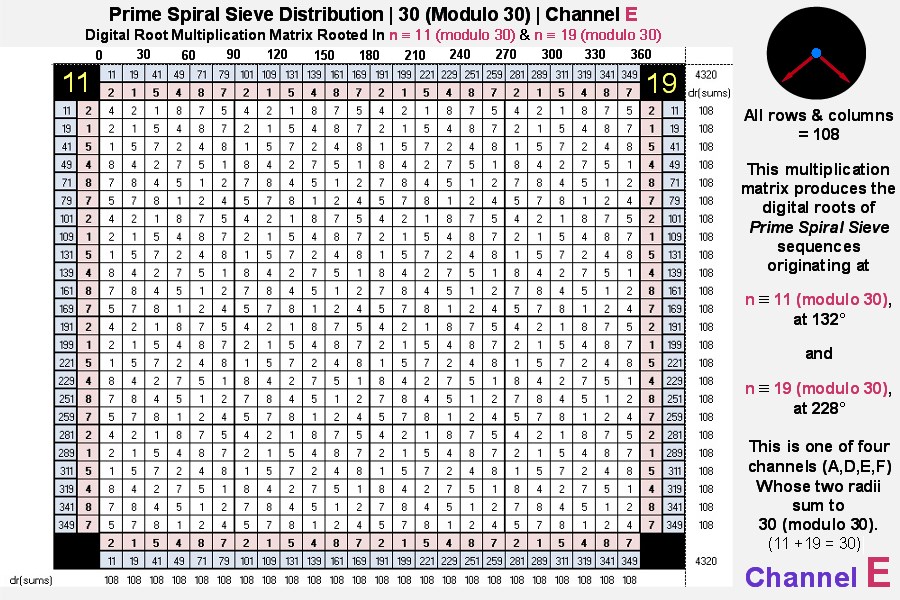
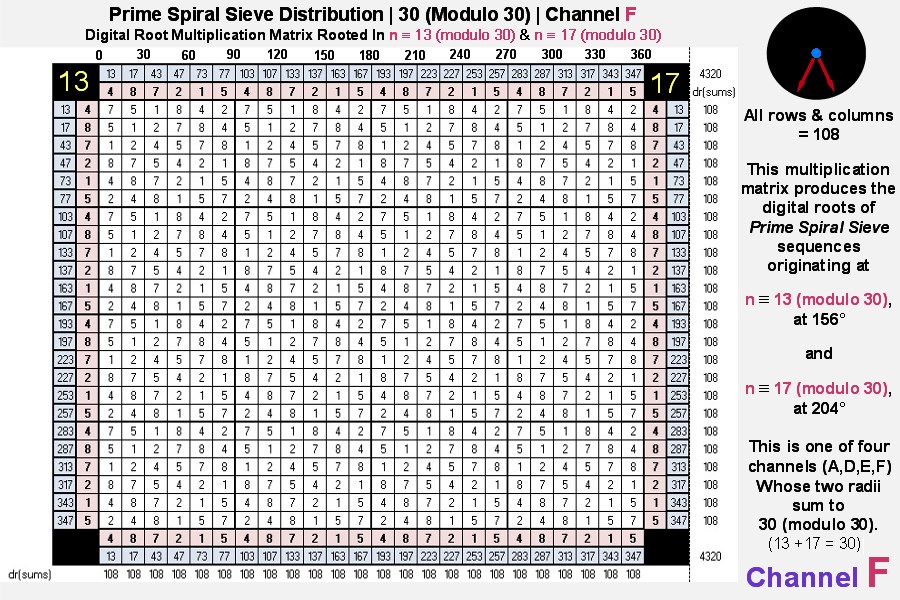
Each of the digital root multiplication matrices produced by the six channels consists of what are known in mathematics
as 'Orthogonal Latin Squares' (defined
in Wikipedia as "an n x n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column"
... in our case every row and column of the repeating 6x6 matrices possesses the six elements: 1, 2, 4, 5, 7, 8 in some order).
Also, the sum of the multiplicative digital roots = 108 x 24 = 2592 = 432 x 6.
[Note: Channels A, D, E and F combined represent the set of natural numbers not divisible by 2, 3 and 5, the first 24 elements
of which form the basis of the Magic Mirror Matrix.]
The graphic below illustrates the transformative relationships between the matrices employing their primary building
blocks (one of the sixteen identical 6 x 6 (36 element) Latin Squares that constitute each matrix):
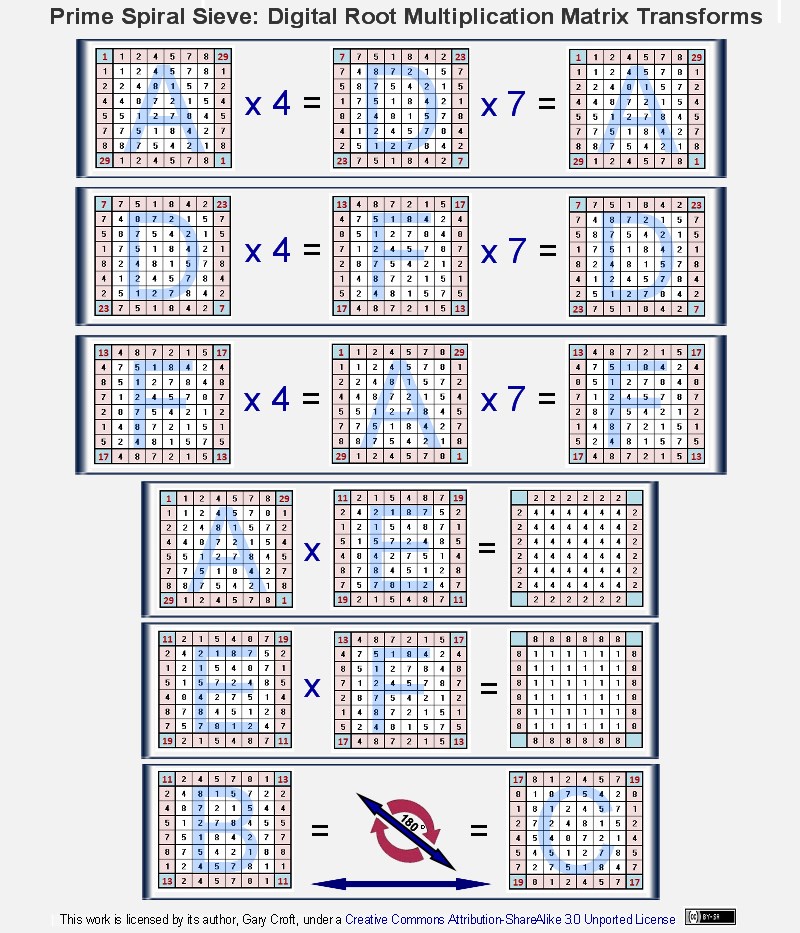
Focusing on just the twin prime distribution channels, we see the relationships shown below [and, directly above, we show
that two of the channels (B & C) transform bi-directionally by rotating 180° around one of their principal (lower-left to upper-right)
diagonal axes]:
Fibonacci Digital Root Multiplication Matrix and Parsing Symmetries
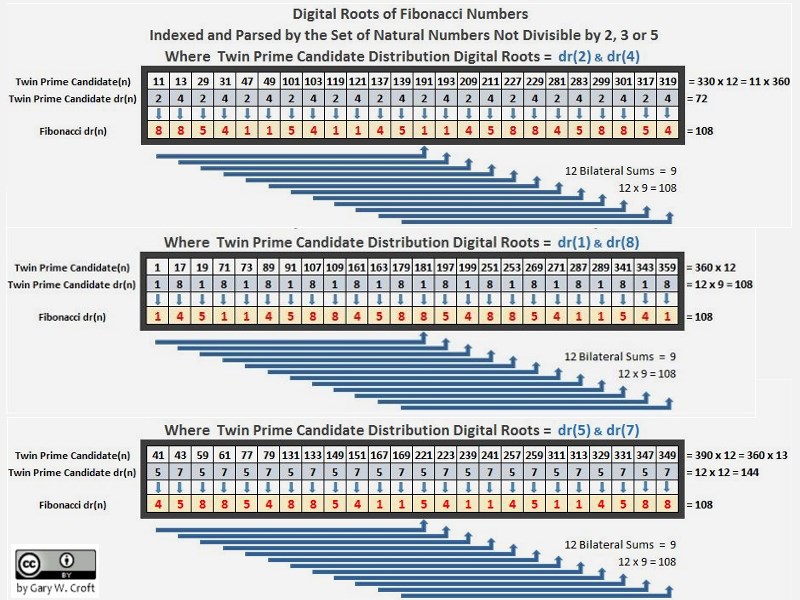
In our discussion under Cirque de Primes, above, we noted that the digital root of Fibonacci numbers indexed by natural numbers not divisible by 2, 3 or 5 form a 32-beat palindromic sequence that repeats every 120° and sums to 432 every 360°. When matrix multiplied this sequence forms a pyramidal mandala of reflectional symmetries that is vertically, horizontally and diagonally palindromic, not to mention each quadrant is palindromic, consisting of perfect symmetry in the form of 8 x 16 x 2 = 256 bilateral 9 sums. Look deeper, and you'll discover yet other vertical and horizontal symmetries. If there were room here, we'd expand this matrix times 3 to encompass 360°. Its 96 palindromic rows and 96 palindromic columns would all equal the magic number 432 ... (We've documented this sequence on the On-Line Encyclopedia of Integer Sequences as A227896.)

When we index the Fibonacci digital roots matrixed above by the twin prime digital root parsing method described earlier, where we parse by digital root dyads {2,4}{1,8} and {5,7}, bilateral sum symmetries are revealed:
To complete the picture (the 4th dimension of our 108 x 4 = 432 geometry), we illustrate the Fibonacci digital root sequencing for the 'Isolated Prime' candidates:
Distribution of Squared Prime Numbers via Fibonacci Digital Roots
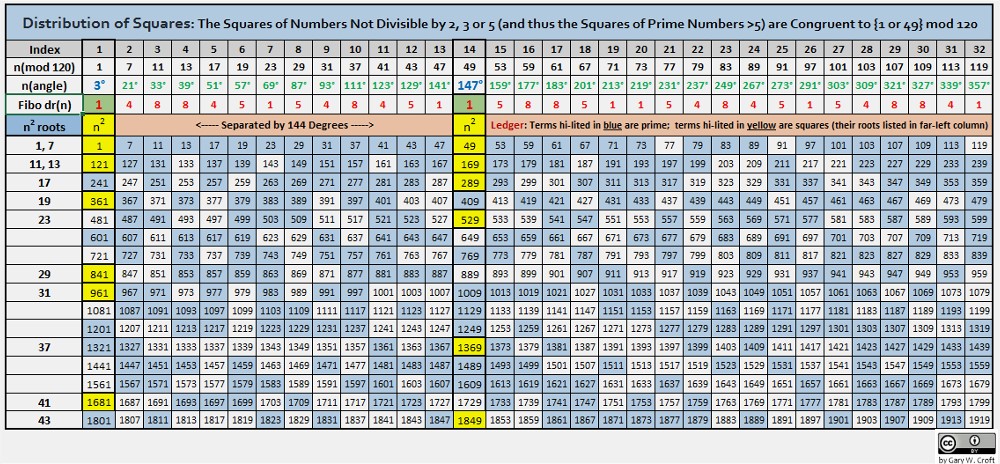
Analysis of the modulo 120 sequences discussed above reveals that the digital root of Fibonacci numbers indexed by squared members of natural numbers not divisible by 2, 3 or 5 is always 1, while the squared numbers they're indexed by are always congruent to either 1 (mod 120) or 49 (mod 120), i.e., The squares of all prime numbers >5 are congruent to {1 or 49} mod 120, as follows (shown in relation to modulo 30):
Squares of n ≌ {1,11,19,29} mod 30 are ≌ {1} mod 120
Squares of n ≌ {7,13,17,23} mod 30 are ≌ {49} mod 120
All prime numbers >5 fall into one of the above two categories. (The author has documented this sequence on the On-Line Encyclopedia of Integer Sequences [Sequence #A227863], where it's named: Numbers congruent to {1, 49} mod 120.). [We can also demonstrate that perfect squares of numbers not divisible by 2, 3 or 5 possess a digital root of 1, 4 or 7 and are congruent to either {1} or {19} modulo 30. More on this at
Distribution of Perfect Squares.]
This sequence is mysteriously prismatic, as prime numbers embedded in squares are split off in two angles (determined by the terminating digits of their factors), i.e., within a modulo 120 factorization wheel where 1 = 3°, the squares distribute to 3° and 147°, and are thus separated by 144° (And we have to ask whether it's coincidental that the digital roots of the Fibonacci numbers that form the 32-beat repeating palindromic sequence also sum to 144, not to mention, as we've already noted above, when the first three twin prime candidate pairs are summed and multiplied together, 24 x 36 x 60 = 51840, and 51840/360 = 144. This last fact will take on even greater significance when we diagram the 'square roots of squares,' second image, below. One more riff on 144: it's the 12th Fibonacci number following 89 and the only Fibonacci number that's a square other than Fibo1. When you divide 144 by 89, a number with magical properties we explore under 'Fibonacci Twins,' below, you produce an approximation of the golden ratio, or phi, with a difference of only +0.000056460660007.). Another fascinating feature of this array is that any even number of–not necessarily contiguous–factors drawn from any one of the 32 angles in this modulo 120 configuration distribute products to 1(mod 120) or 49 (mod 120), along with the squares. Two examples: 1) at 33°: 11 x 131 x 251 x 371 = 134187361, which is congruent to 1 (mod 120) ; ... 2) at 291°: 97 x 217 = 21049, which is congruent to 49 (mod 120). The matrix below illustrates these relationships:
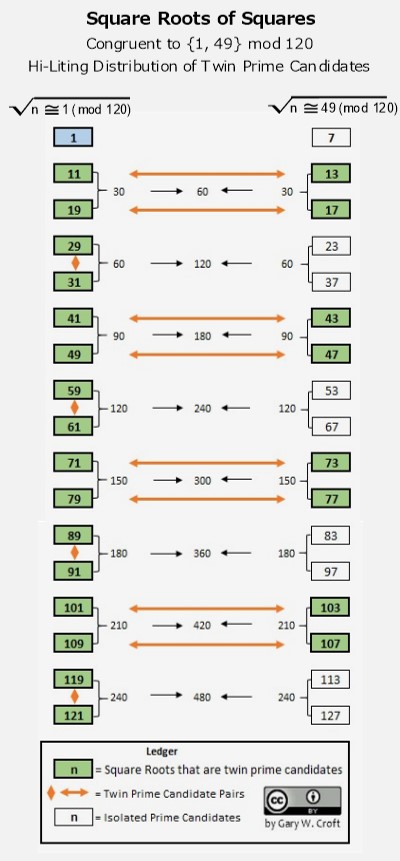
Referencing the matrix above, the illustration below sieves the squares congruent to {1,49} mod 120 and takes their square roots. Twin prime candidates are emphasized to show their repeating zig-zag sequencing on the rungs of a perfectly counter-balanced lattice structure mysteriously populated by the set of natural numbers not divisible by 2, 3 or 5:
Fibonacci Convergence
It is well known that the ratio of any Fibo(n+2)/Fibo(n) will converge to a limit φ + 1 = φ2 (an irrational number) as n approaches infinity (φ being the symbol for phi or the "golden ratio" which = 1.6180339887498948482045868343656 ...). And so it follows that the ratios of the Fibonacci numbers indexed to the twin primes (n and n+2) and/or twin prime candidates in sequence converge accordingly (in other words, the square roots of the ratios of Fibonacci numbers indexed to the twin primes and/or twin prime candidates in sequence converge to φ).
Here are some examples (square roots not taken):
Fibo(13)/Fibo(11) = 2.617977528089887640449438202247 ...
Fibo(19)/Fibo(17) = 2.618033813400125234815278647464 ...
Fibo(31)/Fibo(29) = 2.618033988748203621343798191078 ...
Fibo(43)/Fibo(41) = 2.618033988749894831892914017992 ...
Fibo(49)/Fibo(47) = 2.618033988749894848153928976786 ...
Fibo(61)/Fibo(59) = 2.618033988749894848204586345776 ...
Here's an interesting connection to Fibo(13)/Fibo(11) = 2.617977528089887640449438202247: Fibo(13) = 233, while Fibo(11) = 89. The square root of Fibo(13) divided by Fibo(11) = 122 divided by 89 (and 89 has the basis of the Fibonacci sequence in the decimal expansion of its reciprocal). Then consider that 3 x 122 = 432, a fascinating number we discuss above under 'Cirque de Primes,' below under 'Fibonacci Twins,' as well as on our page detailing the Magic Mirror Matrix where we also examine the amazing properties of number 89.
Perfect Twins
One other twin prime related deterministic algorithm worth noting stair-steps its way up the twin prime
distribution channels with a periodicity of 6. We've dubbed these "perfect twins," given that the square root of their
'perfect' square sums is the first perfect number, 6, or one of its multiples. To calculate this interesting twin pair candidate sequence,
start with x = 6 (then add 6 and repeat for each successive step, as shown below):
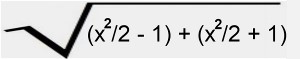
x=6: 62 = 36; 36/2 = 18; 18-1 = 17; 18+1 = 19; thus, twin pair candidates = 17 and 19; take the square root of 17+19
which = 6
add 6 (6+6 = 12)
x=12: 122 = 144; 144/2 = 72; 72-1 = 71; 72+1 = 73; thus, twin pair candidates = 71 and 73; take the square root of 71+73
which = 12
add 6 (12+6 = 18) {repeat ... n}
The table below shows the first 20 steps in the sequence. All "perfect twins" are hi-lited in gold. The table is arrayed in five columns to show the +30 and repeating modulo 30 vertical incrementation. Also note that the digital roots for all prime pair candidates and/or prime pairs in this sequence equate to 8 + 1 = 9, e.g., 17, or dr(8) + 19, or dr(1) = 36 or dr(9).
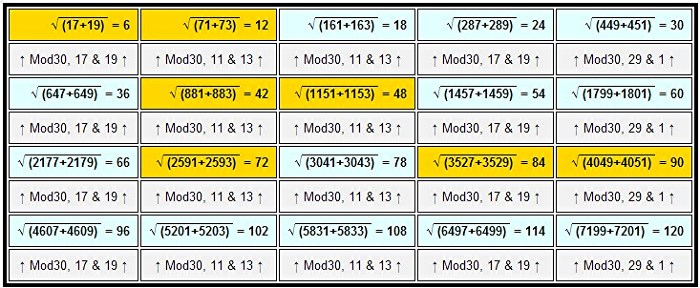
[Note: We've documented these "perfect twins" on the On-Line Encyclopedia of Integer Sequences (Sequence #A232878) where they're defined as Twin prime pairs which sum to perfect squares.]
Infinite Twins
Referencing the Twin Prime Conjecture: Given that
all composite numbers extant in the infinite set of natural numbers not divisible by 2, 3 or 5 (which by definition contains all prime numbers ≥ 7 and their multiplicative multiples and is defined as n ≌ {1, 7, 11, 13, 17, 19, 23, 29} modulo 30 and sequences as 1 {+6 +4 +2 +4 +2 +4 +6 +2} {repeat ... ∞}), can be identified algorithmically, employing eight geometrically-expanding factorization sequences, ultimately leaving the equal distribution of all prime numbers ≥ 7 ... n along eight diagonals (and we note here that, regardless, according to a theorem due to Dirichlet any arithmetic progression with no common factor throughout contains infinitely many primes); and given that six of these diagonals with an infinity of primes form the three twin prime distribution channels (described above), which, when combined into a single number line, account for all twin primes > (5,7). This sequence is defined as n ≌ {1, 11, 13, 17, 19, 29} modulo 30 and has a repetition cycle of 1 {+10 +2 +4 +2 +10 +2} {repeat ... ∞} where every 6 beats produces 3 pairs of n, n+2 twin prime candidates.
Given these facts, it would seem axiomatic that there are infinite prime pairs in the form p, p + 2. (Cautionary Note: We are not sufficiently delusional to consider this a mathematical proof. Rather, this statement is an argument for the high probability that the number of twin primes is unnumberable, i.e., infinite.)
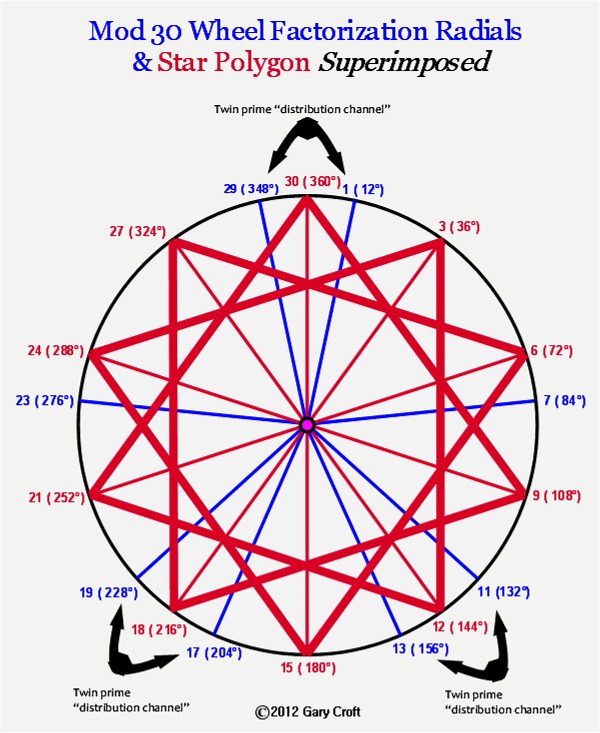
Seeing Stars
Another interesting aspect of the three twin prime distribution channels becomes apparent when the eight radials of the Prime Spiral Sieve (or modulo 30
wheel factorization), are superimposed upon a {10/3} regular star polygon (see illustration, below). Thirty (30)
is the total unit length of the ten straight line segments used to construct the {10/3} star polygon, where the straight lines connect every 3rd point of 10 equally spaced
points lying on a circle's circumference. Note that three points of the polygon, 144°(12), 216°(18) and 360°(30), precisely and symmetrically split the
twin prime distribution channels. And as you rotate this object, several other symmetries become apparent, e.g.: between 7 → 17; 13 → 23; and 7 → 23.
Even more interesting, is the result when you superimpose a 15-point star over a Prime Spiral Sieve with its 'aperture' increased to modulo 90. As shown below, every one of the 9 twin prime distribution channels is hit dead center by points of the star:
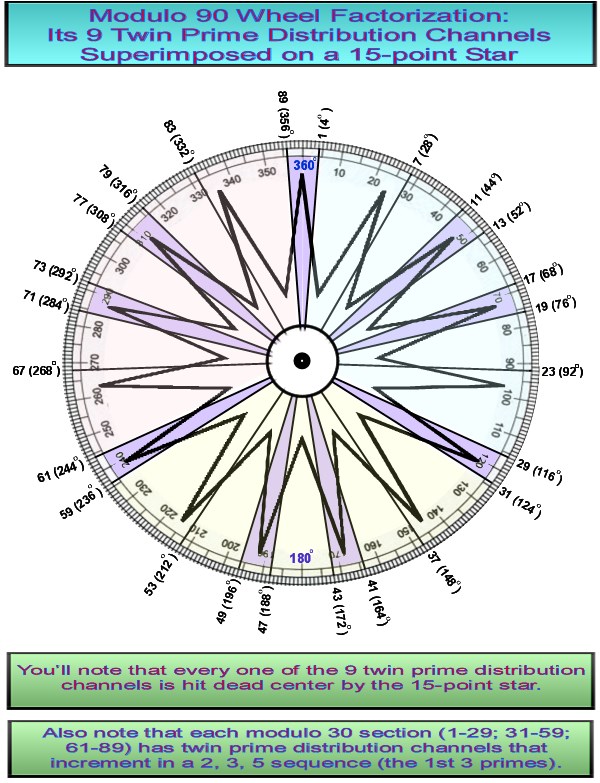
This superimposition reveals some interesting circularities: When you sum the 9 angles that hit the twin prime distribution channels dead center you get 1800. 1800/360=5; 1800/9=200. In turn, sum the 6 angles that hit equidistant between the twin prime distribution channels and you get 1080. 1080/360=3. 1080/6=180. In toto, 1800+1080=2880; 2880/360=8.
Twin Prime Magic Squares
Before leaving the twin primes, let's take one more look at them from a digital root perspective. The illustration
below shows the infinitely repeating digital root sequences for each of the 8 radii of the spiral sieve, as well the sums of
the digital roots (in yellow) between each radius, including the twin prime distribution channels. It's notable that the twin
pair digital sum sequences, {3,9,6}, {9,6,3} and {6,3,9} when positioned adjacent to each other in ascending order, create a
"magic square" (in that all vertical, horizontal and principal diagonal sums equal 18), as pictured below:
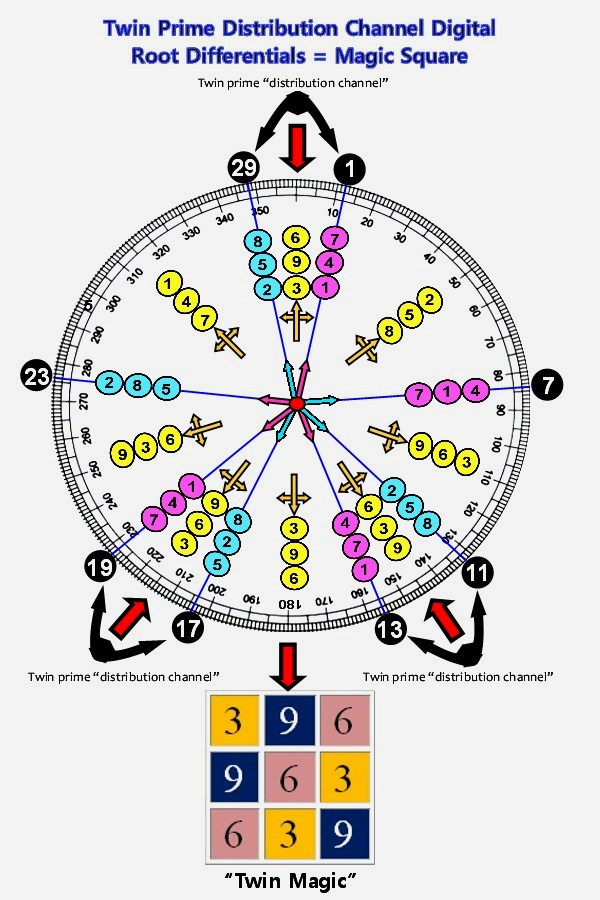
The {3,6,9} triangulation is a member of the so-called 'Trinity of Triangles,' along with {1,4,7} and {2,5,8}. Looking at the graphic above, you'll note that each of the three Twin Prime Distribution Channels has one leg that sequences as {1,4,7} and the other as {2,5,8}, albeit the starting digits may vary, viz. {1,4,7} vs. {4,7,1}. When you combine the three legs that sequence as {1,4,7} as well as the three legs that sequence as {2,5,8}, these also form magic squares, as illustrated below. Another magic square hidden in plain sight becomes evident when you examine the sequences you encounter in rotation: {1,4,7} ... {2,5,8} ... {3,6,9} in various sequence combinations. Taking the digits 1 thru 9 these three triangles represent, they can be configured into a magic square representing 'et alia', in this case the famous 'Lo Shu Magic Square':
Under "Factorization Algorithms for the Twin Prime Candidates," above, we detailed how twin primes come in three digital root configurations: {2,4}, {5,7} and {8,1} and demonstrated that these dyads, in turn, can form the basis of period-24 digital root cycles that generate {9/3} star polygons via 3 x 3 matrices. So with these cycles and matrices in mind, take the three twin prime digital root dyads under discussion, sequence their 24-length digital root cycles, then tier them, and you'll discover a direct means to constructing the Trinity of Magic Squares via the Trinity of Triangles, as illustrated here:
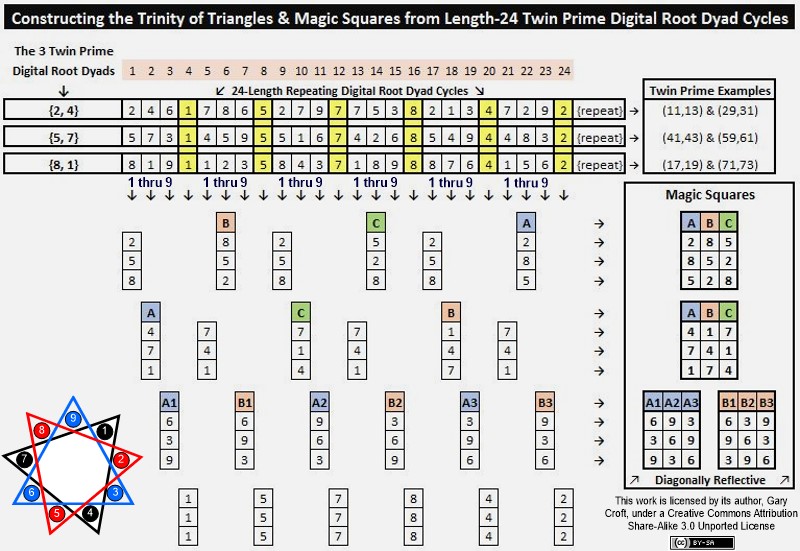
When you rotate either the {1,4,7} or {2,5,8} magic square around its horizontal axis, i.e. columns {A,B,C} become {C,B,A}, then add the {1,4,7} {2,5,8} magic squares together, you produce a square with nine 9's. For example, adding the first rows of each gives us: {2,8,5} + {7,1,4} = {9,9,9}.
Triangles and magic squares similar–or identical–to those shown above can be derived from the digital root sequence cycles of all three twin prime distribution channels (namely numbers ≌ to {11,13}, {17,19} and {1,29} modulo 30). This is also true of dyads formed by paired radii of the Prime Spiral Sieve that sum to 30, i.e., numbers ≌ to {1,29}, {7,23}, {11,19}, or {13,17} modulo 30, as well as dyads formed when {n, n + 10} are ≌ to {1, 11}, {7, 17}, {13, 23} or {19, 29} modulo 30 (note their pairing by terminating digits). One example relating to twin primes: The first three candidate pairs in the twin prime distribution channel ≌ to {11,13} modulo 30 (all three of which are indeed twin primes) sequence their digital roots as follows:
{11,13} = digital roots 2 & 4
{41,43} = digital roots 5 & 7
{71,73} = digital roots 8 & 1.
As you can see, this is the same digital root sequence illustrated above.
It appears that the triangulations and magic squares structuring the distribution of twin primes (and as it turns out, all prime numbers) have a genesis in universal principles involving symmetry groups rotated by the 8-dimensional algorithms discussed at length on this site. You can see this universal principle at work, for example, with regard to the Fibonacci digital root sequence when coupled to a pair of dyads that follow certain incremental rules. As we illustrated above, the initializing dyad of the period-24 Fibonacci digital root sequence is {1,1, ...}. We can generate triangles and magic squares by tiering the Fibonacci digital root sequence with two pairs of terms that are + 3 or + 6 from the initial terms {1,1}. The values of the 2nd and 3rd tiers, or rows, must differ, or symmetry is lost. In other words, the first two columns should read either {1,4,7 + 1,7,4, or vice versa} but not {1,4,7 + 1,4,7, or 1,7,4, + 1,7,4}. Here's a picture that displays the {1,4,7 + 1,7,4} digital root sequencing used to construct triangles and magic squares:
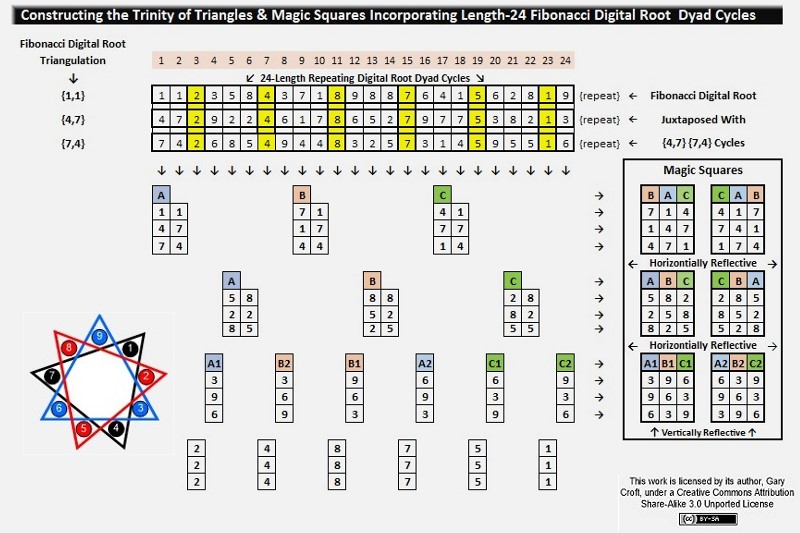
We'll end our exploration of twin primes with two powerful magic squares. First: The Trinity of Magic Squares x 3 can be constructed into a magic square where all columns, rows and principal diagonals equal 45 (and were you to construct an 8x8 square employing 64 Trinity Magic Squares shown below, all columns, rows and principal diagonals would equal 360).

Next we show how the Lo Shu Magic Square and Trinity of Magic Squares can be combined in a "4-Fold Way" to create their own magic square when configured in a 4 x 4 matrix of magic squares consisting of 144 elements where all rows, columns and principal diagonals sum to 60
and the sum total of the matrix's elements = 720 = 360 x 2 (and were we to construct a 6x6 square employing 36 4-Fold Way Magic Squares shown below, all columns, rows and principal diagonals would equal 360).

Return to www.primesdemystified.com Home Page
Your feedback welcome! Email: gwc@hemiboso.com