This work is licensed by its author, Gary William Croft, under a Creative Commons Attribution-ShareAlike 3.0 Unported License
Welcome to the most comprehensive review of the number 30 ever created. The number 30 possesses remarkable attributes, including–and perhaps most profoundly–its role (along with its prime factors 2, 3 and 5) as a primary organizing principle in the distribution of prime numbers. Before getting to that, here's a list of mathematical properties and other interesting facts relating to this integer:
- 30 is a natural number (aka whole number; counting number; non-negative integer; positive integer) following 29 and preceding 31.
- 30 is a positive whole number with two digits.
30 is the 19th composite number (aka nonprime number; non-negative nonprime; natural nonprime; whole nonprime; counting nonprime).
- 30 is an even number.
- 30 is equal to: 2 + 4 + 6 + 8 + 10; 4 + 5 + 6 + 7 + 8; 2 + 3 + 5 + 8 + 12; 6 + 7 + 8 + 9; and 1 + 4 + 9 + 16.
30 is divisible by 1, 2, 3, 5, 6, 10, 15 and 30; its divisors sum to 72; it is thus congruent to 2 mod 4: a(n) = 4n+2, i.e., is an integer possessing equal numbers of odd and even divisors (aka singly even numbers).
30 is the 3rd primorial (2∗3∗5); the first two being 2 (1∗2) and 6 (2∗3). It follows that all primorials ≥ 30 are evenly divisible by 30.
- 30 is the smallest sphenic number; divisible by exactly 3 distinct primes (2, 3 and 5) and a total of 8 divisors (see bullet, directly above).
- 30 is the smallest of the four terms in the arithmetic progression of positive integers possessing three distinct prime factors: 30-66-102-138.
- 30 is smallest number not the sum of three integer cubes.
- 30 is equal to multiples of the first three prime numbers, namely:
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 15∗2 = 30
3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 10∗3 = 30
5 + 5 + 5 + 5 + 5 + 5 = 6∗5 = 30
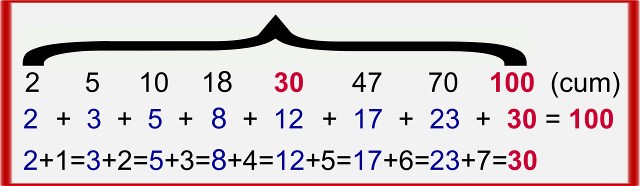
- 30 is a square pyramidal number in that it is the sum of the first four square numbers (1² + 2² + 3² + 4² = 30), as illustrated below:
- 30 is an octagonal pyramidal number: n(n+1)(2n-1)/2.
- 30 is a 5-smooth number (aka Hamming sequence) in that its prime divisors are all ≤ 5.
- 30 is a 7-smooth number (aka highly composite number or humble number) in that its prime divisors are all ≤ 7.
- 30 is an 11-smooth number in that its prime divisors are all ≤ 11.
- 30 is the product of the first 5 nonzero Fibonacci numbers (F1, ..., F5), thus: 1∗1∗2∗3∗5 = 30.
- 30 is equal to (1+5)+(2+5)+(3+5)+(4+5) = 6+7+8+9 = 30
- 30 is equal to 12 + 22 + 52.
- 30 is equal to 25-2 and n5-n is divisible by 30.
- 30 is a pronic number (aka oblong, rectangular or heteromecic number) and as such is the sum of two triangular numbers.
- 30 is the smallest Giuga number.
- 30 is the sum of two successive primes: 13+17=30.
- 30 is the index number for Fibonacci number, F30 = 832040 = 5∗11∗23∗31∗61 = the largest Fibonacci number with 6 digits.
- 30 is the smallest integer with three distinct prime divisors.
30 "splits" twin primes 29 and 31, the latter both a Mersenne prime and a lucky number. This relationship can also be expressed as 30 = average of twin primes 29 and 31 or as
30 is an abundant number (aka excessive number) in that the sum of its divisors (72) exceeds 2n. 30's abundance is thus calculated as: 72 - (2∗30) = 12.
- 30 is a highly abundant number.
- 30 is a member of the Lower Wythoff sequence.
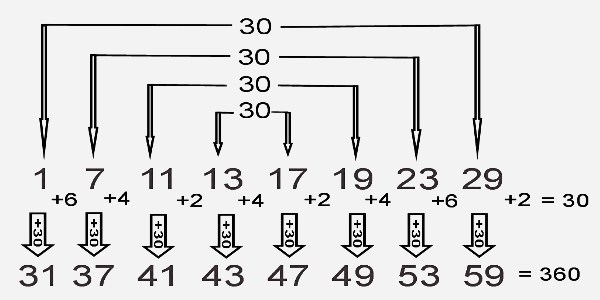
30 is the largest number such that all smaller numbers prime relative to it are actually 1 or prime; those numbers being: 1, 7, 11, 13, 17, 19, 23 & 29. 30 is thus the largest member of the 10-element sequence of very round numbers (the other 9 elements in this sequence being 1, 2, 3, 4, 6, 8, 12, 18 & 24) a reduced residue system consisting of only primes and 1. In 30's case the reduced residue is expressed as {30,{1, 7, 11, 13, 17, 19, 23, 29}}.
- 30 is the number of ways to color a cube with 6 colors.
- 30 has an aliquot sum of 42.
- 30 is a semiperfect number (aka pseudoperfect number) in that a subset of its divisors (5, 10 and 15) = 30.
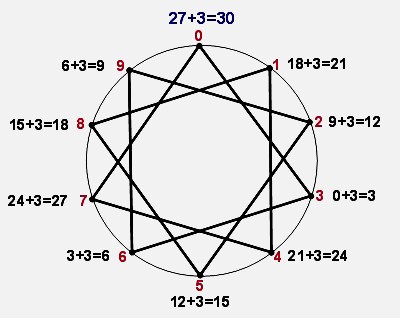
30 is the total unit length of the straight line segments used to construct a star polygon notated as {p/q} where p=10 and q=3 (q is termed the density of the star polygon; in this case the straight lines connect every 3rd point of 10 equally spaced points lying on a circle's circumference.); thus {10/3}. The Schläfli symbol for this polygon is {30}. Illustration, below:
- 30 is the number of sides possessed by the triacontagon (a polygon).
- 30 is the maximum number of edges that may be had by a regular convex polyhedron (aka convex polytope).
- 30 is the number of edges possessed by two of the five Platonic solids: the icosahedron and the dodecahedron.
- 30 is the number of identical vertices possessed by the icosidodecahedron, an Archimedean solid.
- 30 is the number of square faces (along with 20 triangular and 12 pentagonal faces) used to construct the symmetrical Archimedean solid called a rhombicosidodecahedron.
- 30 is the area and perimeter of one of only two Pythagorean triangles whose areas equal their perimeters (5-12-13 and 6-8-10). This can also be termed: 30 is the ordered area and ordered perimeter of a primitive Pythagorean triangle.
- 30 is the number of isohedra.
- 30 is the smallest acute angle in a right triangle whose hypotenuse is twice as long as one of its sides.
- 30 is the 15th member of a sequence quantifying the number of polygon edges constructible with ruler and compass.
- 30 is a twice hexagonal number of the form 2n(2n-1) where n=3.
- 30 is a squarefree integer; not divisible by a square greater than 1, i.e. all of its prime factors are distinct.
- 30 is a cubefree integer; not divisible by any cube > 1.
- 30 is a golden-3 almost prime given that 2∗3∗5=30 and that the products of both 2∗3=6 and 3∗5=15 are golden semiprimes.
- 30 is a 11-gonal number (aka hendecagonal number) of the form n(9n-7)/2.
- 30 is the 20th partial sum of the Kolakoski sequence.
- 30 is a number n such that the sum of its digits squared is a square: 302 = 900 = 9+0+0= 9 or 32.
- 30 is the Least Common Multiple (LCM) of the set 2, 3 and 5 making it the LCM of its own prime factors.
- 30 and its multiples (60, 90, 120 ... n) are the only natural numbers divisible by 2, 3 and 5.
- 30 is the sum of the 32nd Fibonacci number's digits; F32 = 2178309; 2+1+7+8+3+0+9=30.
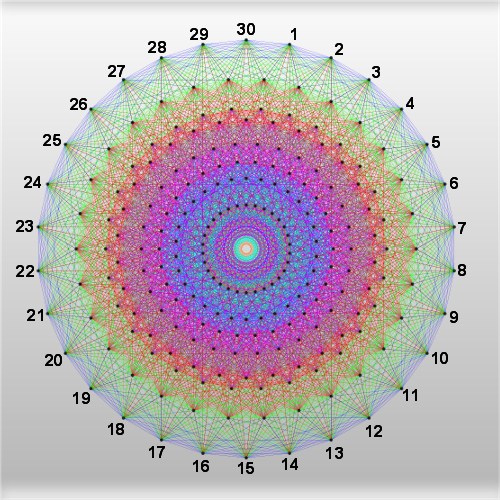
30 is the Coxeter Group number h, dual Coxeter number and the highest degree of fundamental invariance of the Lie Group E8. You'll note, looking at the graphical representation of E8 (see image at top of this page) that the perimeters of every one of its multiple concentric circles possesses 30 points. E8 has 2-, 3- and 5-torsion, and its exponents are the co-primes up to 30, i.e., 1, 7, 11, 13, 17, 19, 23, and 29.
The graphic below superimposes an image of E8 with a star polygon and the 8 radii of a modulo 30 factorization wheel:
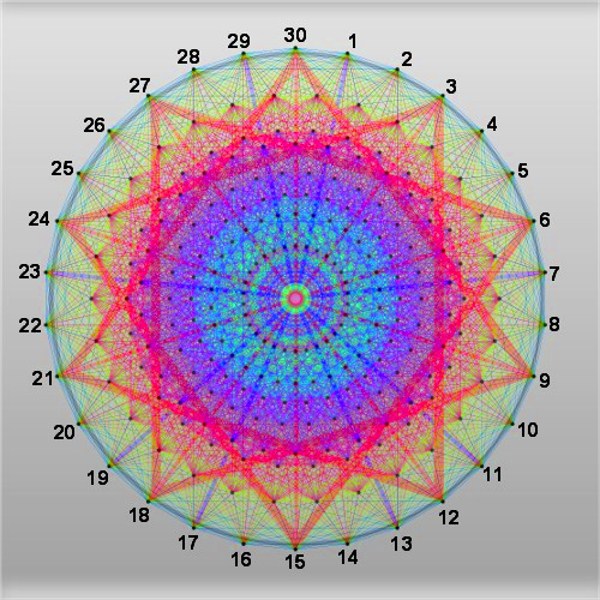
The Number 30 in Lie Group E8: This graphic superimposes images of the star polygon, modulo 30 wheel factorization radii and "E8 graph of the Gosset 421 polytope as a 2-dimensional skew orthogonal projection inside Petrie polygon ... an emulation of the hand drawn original by Peter McMullen" licensed by Creative Commons; license terms here.
- 30 is the number of integer partitions of the number 9: P(9)=30.
- 30 has 296 partitions into distinct parts: P(30)=296.
- 30 in binary form: 111102.
- 30 is an evil number, mathematically speaking, in that it has an even number of 1's in its binary expansion.
- 30 is a dopey number because its binary representation ends in an odd number of zeros.
- 30 is a Harshad number (aka Niven number) in that it's divisible by the sum of its digits.
- 30 is a practical number.
- 30 is an admirable number.
- 30 is a balanced number.
- 30 is a swinging factorial.
- 30 is a polite number, i.e. is the sum of two or more consecutive integers, namely: 4 + 5 + 6 + 7 + 8 = 30.
- 30 is a skinny number in that when squared using "long division" there are no carries.
- 30 is a single number (aka isolated number).
- 30 is a sloping binary number.
- 30 is a Zumkeller number.
- 30 is a permutational number.
- 30 is an idoneal number (aka suitable or convenient number) after Euler's "numerus idoneus".
- 30 is a number having no prime gaps in its factorization.
- 30 is a triangular matchstick number: 3n(n+1)/2; 3∗4(4+1)/2=30
- 30 is a number of the form a2 + 5b2 with a and b as positive integers. Thus, when a = 5 and b = 1: 52 + 5(12) = 30.
- 30 is the 13th value of the sequence: numbers that are not powers of primes.
- 30 is the 3rd value in the sequence: 1n + 2n + 5n.
- 30 is the 3rd value for n in this sequence: n!/24.
- 30 is the 4th value in this sequence (n=3): n3+n; 33+3=30
- 30 is the 4th value in this sequence (n=3): n(n+1)(n+2)/2; 3(3+1)(3+2)/2=30.
- 30 is the 4th value in this sequence (n=3): n(n+7); 3(3+7)=30.
- 30 is the 4th value in this sequence (n=3): (n/2)∗(3∗n + 11); (3/2)∗(3∗3+11)=30.
- 30 is a number such that the number of its prime factors counted with multiplicity (3) is prime.
- 30 is a number such that the sum of its prime factors counted with multiplicity (2 + 3 + 5 = 10) is not prime.
- 30 is a number n such that primorial(n)/2 + 16 is prime.
- 30 is a number n such that primorial(n)/2 - 16 is prime.
- 30 is a number n such that n2+(n-1) is prime; 302+(30-1)=929 (prime).
- 30 is a number n such that n2+(n+1)2 is prime; 302+(30+1)2=1861 (prime).
- 30 is a number n such that n!+2/2 is prime.
- 30 is a number n such that 2(n+1)- 1 is prime, thus: 2(30+1)- 1 = 2,147,483,647 (prime).
- 30 is a number n such that 6n-1 and 6n+1 are twin primes.
- 30 is a number n such that 2n-1 is prime; 2∗30-1=59.
- 30 is a number n such that 2n+1 is prime; 2∗30+1=61.
- 30 is a number n such that n3+n+1 is prime.
- 30 is a number of the form x2 + y2 + z2, where x, y & z are ≥ 0 (and in this case 12 + 22 + 52 = 30).
- 30 is a 4-dimensional figurate number.
- 30 is a hypotenuse number in that its square is the sum of 2 distinct nonzero squares: 182 + 242 = 302 or 324 + 576 = 900.
- 30° = π/6 radians = (π/6)r.
- 30 has a digital root (aka repeated digital sum) of 3: 3+0=3. And, its digit sum also equals 3.
- 30 has five 1's in its base-φ representation.
The number 30, when plugged into Euler's totient function, phi(n): phi(30)= 8, with the 8 integers smaller than and having no factors in common with 30 being: 1, 7, 11, 13, 17, 19, 23 & 29. Thirty is the largest integer with this property.
- Modulo 30 of all prime numbers (with the exception of 2, 3 and 5) must be 1, 7, 11, 13, 17, 19, 23 or 29.
- Modulo 30's quadratic residues (making them congruent with perfect squares) are 1 and 19.
- Below is a magic square where all horizontal, vertical and corner-to-corner diagonal sums total 30 (created by Gary Croft on 17 March, 2012). Explore its beautiful symmetries involving 10's:
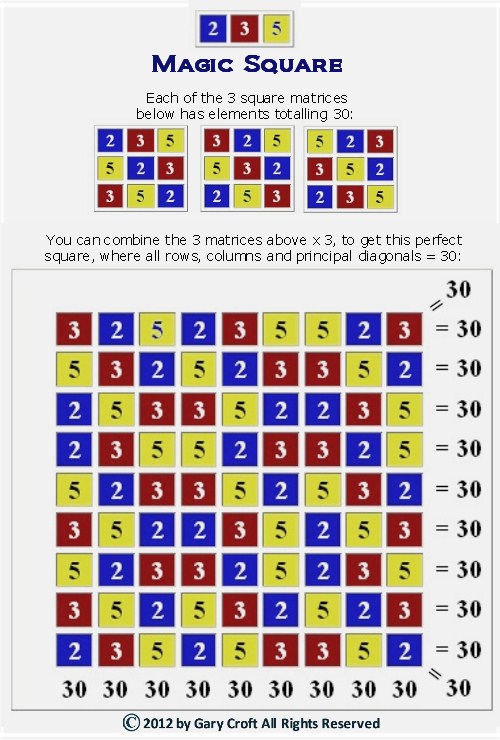
- Here's another magic square with rows, columns and principal diagonals totalling 30; in this case the first three prime numbers {2,3,5} are configured into 3 square matrices (each containing three 2's, 3's and 5's) which in turn are multiplied times three to make magic (created by Gary Croft on 25 April, 2012):
When arrayed in eight columns, the set of all natural numbers not divisible by 2, 3 and 5 (which by definition consists of 1 and all prime numbers >5 and their multiples) possesses perfect symmetry involving the number 30, as illustrated below. [Also note that the sum of the digital root sums (1 + 7 + 2 + 4 + 8 +1 + 5 + 2) of the first 8 elements in this set (1, 7, 11, 13, 17, 19, 23, 29) = 30.]:
When twin primes and twin prime candidates ≥ (11, 13) are arrayed in this divergent (aka harmonic) sequence: 11{+2+4+2+10+2+10} {repeat ... n}, the intervals between them (2+4+2+10+2+10) total 30, as shown in the matrix below. (Click this link for a deep exploration: twin primes.)
= Prime = Interval = Composite
prime +2 prime = Prime Pair
- 30 is interesting when contextualized within the set of natural numbers 1-100 (Hint: Start with the bottom row, then work up.):
- 30 is often cited as the "sweet spot" for optimizing sample size.
- 30 is the distance in degrees between the numbers on a clock.
- 30 is the total number of major and minor keys in Western tonal music, including enharmonic equivalents.
- 30 is the number of upright stones that originally encompassed the Sarsen Circle, Stonehenge's best known feature.
Number Thirty (30): Organizing Principle of the Prime Number Sequence
The integer thirty (30), provides both vertical and horizontal structure (a beautifully symmetrical superstructure, if you will) to the prime number sequence. For a detailed description and graphic representation of this integral dimension of the primes, go to Prime Spiral Sieve.
References:
- Wikipedia's page for The Number 30.
- VirtueScience.com's take on The Number 30.
- RichardPhillips.org's page for The Number 30.
The work of exceptional amateur mathematician Philip G Jackson at www.simplicityinstinct.com further corroborates the importance of the number 30. He has defined new prime number attributes and shows how what he calls "Prime Number Channels" provide a simple structure for understanding the pairing of primes in Goldbach's Strong Conjecture.
- For an interesting discussion of the "magic" properties of number 30, check out Clif Droke's essay here.
- Using standard deviation confidence intervals, statistician Jed Campbell explains why 30 is often cited as the "sweet spot" for optimizing sample size.
This work is licensed by its author, Gary Croft, under a Creative Commons Attribution-ShareAlike 3.0 Unported License
To contact the author, email gwc@hemiboso.com.[Note: Logo graphic at header of this page incorporates image of "E8 graph of the Gosset 421 polytope as a 2-dimensional skew orthogonal projection inside Petrie polygon. It is an emulation of the hand drawn original by Peter McMullen." The image is licensed by Creative Commons. For license terms click here.]
Return to www.primesdemystified.com Home Page