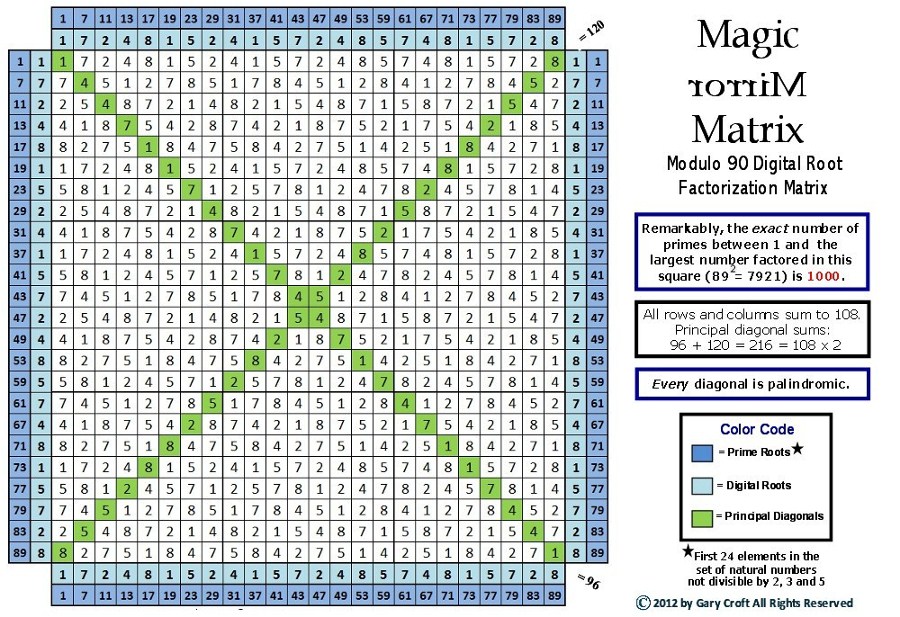
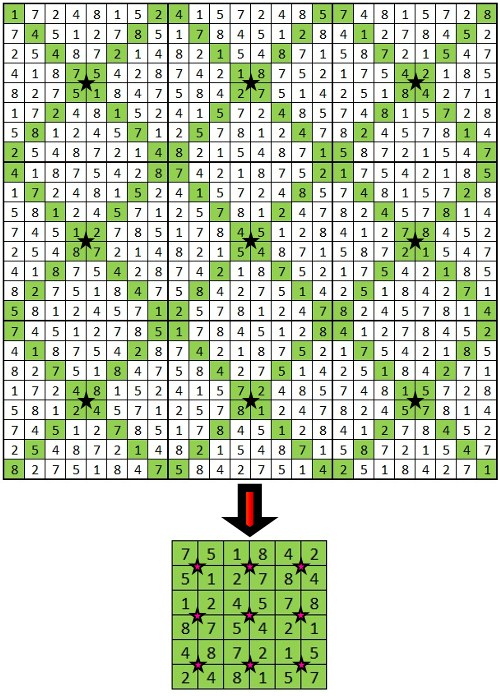
The Magic Mirror Matrix is a geoarithmetric object that maps a dense compaction of perfectly balanced bi-lateral symmetries expressed at the digital root level. Fundamentally, the matrix serves as a calculatory
geometry that factorizes and accounts for all prime numbers ≥ 7.
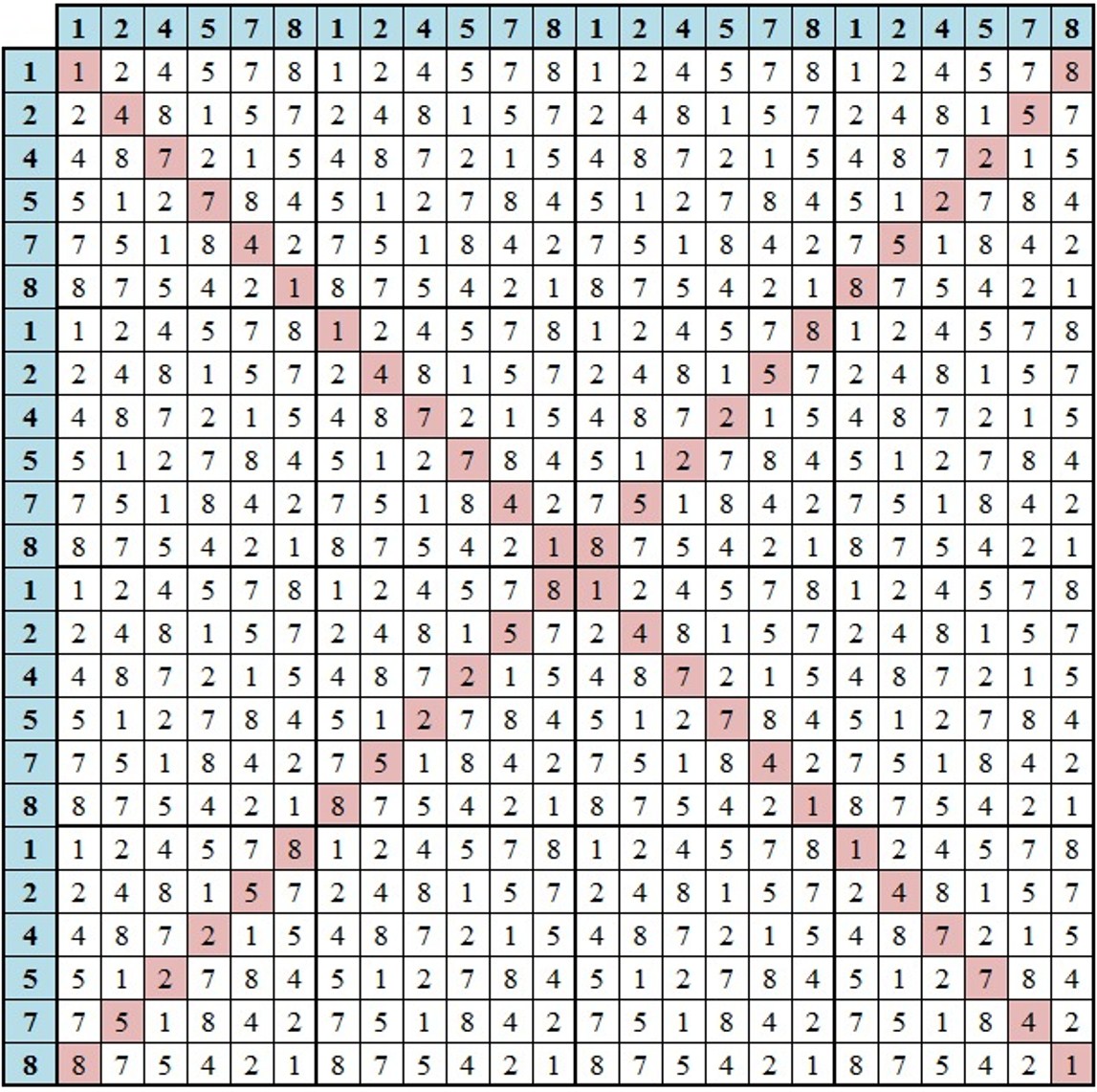
The matrix is rooted in the first 24 elements from the set of natural numbers not divisible by 2, 3 and 5, which starts with 1 and ends
with 89. When these 24 elements are factorized sequentially against themselves and the products are converted to digital roots,
e.g., 7 x 7 = 49 = 4 + 9 = 13 = 1 + 3 = dr(4), the Magic Mirror Matrix results. You might call this a Vedic Square on steroids (and in fact, as we shall demonstrate below, the Magic Mirror Matrix and the Vedic Square have a deep, organic affinity).
This matrix, aside from serving as a digital root calculator and possessing origin (aka reflectional) symmetry (rotate the matrix 180 degrees and the original sequence is reflected mirror-like), and aside from the fact that every diagonal is palindromic and that every row and column sums to 108 and possesses 12 bi-lateral sums totaling 9, and that the {1,4,7} and {2,5,8} members of the so-called "Trinity of Triangles" (see below) parse along the principal diagonals, which together have their own dance of bi-lateral 9's, and aside from its deep connection to the Vedic Square, this matrix represents the set of factorizations that result in the first 1000 prime numbers (and we mean exactly 1000). In fact, as we've already suggested, this geometry–when its sequences spiral deterministically to infinity–accounts for the
factorizations of all composite numbers in the set of natural numbers not divisible by 2, 3 and 5, leaving all
prime numbers ≥ 7. These factorizations are derived from the 8-dimensional Prime Spiral Sieve methodology.
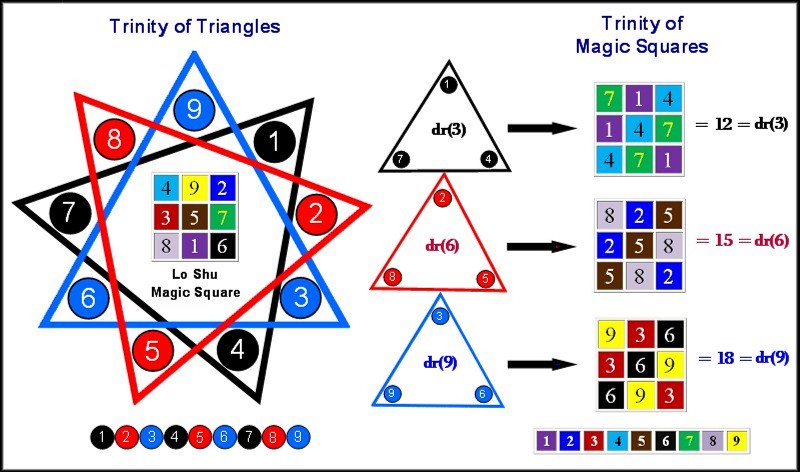
This object was conceived after studying the infinitely repeating digital root sequences involving the Trinity of Triangles derived from
a 9-pointed star: {1,4,7}, {2,5,8} and {3,6,9} and its related Trinity of Magic Squares, within which are embedded triangular rotation
sequences:
To best appreciate the symmetry, rotate the matrix 90 degrees either clockwise or counter-clockwise so that the
corner-to-corner diagonals form a cross. When you do so, the two perfect symmetries that reflect those diagonals will become readily apparent,
demonstrating symbolically the perfectly balanced yin-yang relationship between the {1,4,7} and {2,5,8} members of the Trinity of Triangles
(and we should note here that the squares of all members of this set have digital roots of either 1, 4 or 7, and in fact this is true of all
prime numbers except 3). Why is 3 distinct in this regard? It's consistent with the fact that 3 and its multiples {3,6,9 ...} account for
structure in our domain, within which the {1,4,7} and {2,5,8} triangles interact in a spiraling algorithmic dance. For example,
the Magic Mirror Matrix pictured above (think of it as a module with sub-modules, or, if you will, a modulo with sub-modulos) has 9 modulo
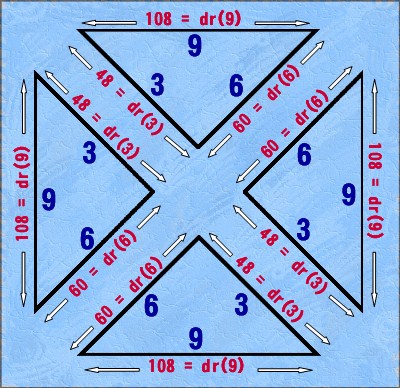
30 divisions that cascade in three rows of three to complete a modulo 90 cycle, viz. {3,6,9}. Less obvious, but even more telling in this
regard, are the {3,6,9} structural relationships revealed when the line elements of the four right-angled Isosceles Triangles created by
the two principal diagonals are summed and digitally rooted, as illustrated, below:
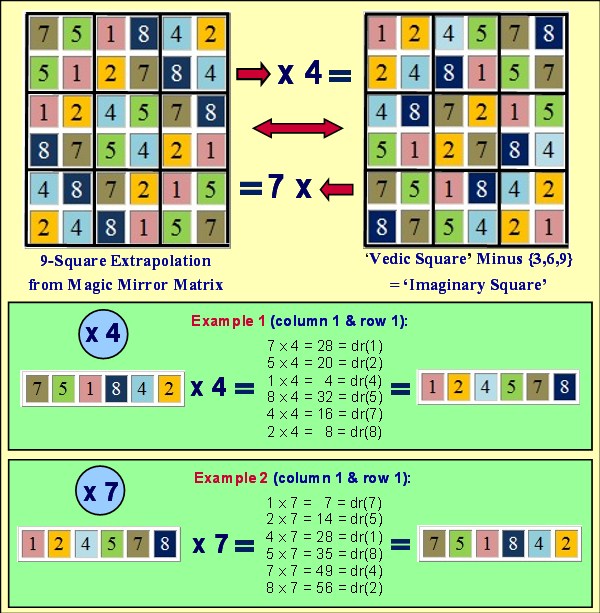
The Reciprocal Magic Mirror Matrix ↔ Vedic Square Transformation
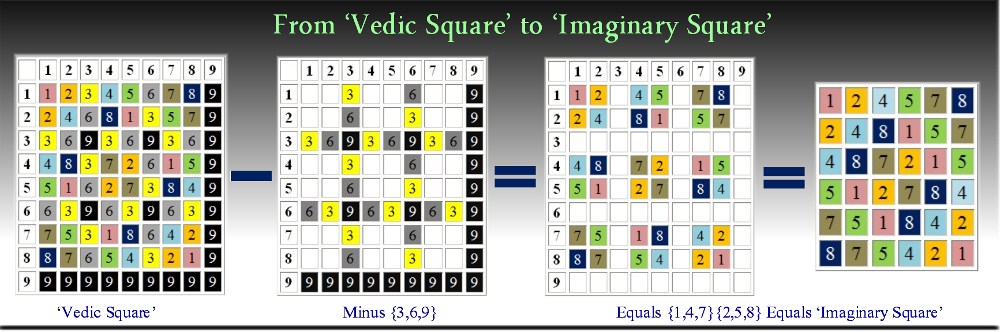
As noted previously, another interesting aspect of the Magic Mirror Matrix is that it has a deep affinity with the Vedic Square. Namely, if you hi-lite the
principal diagonals in each of its 9 modulo 30 partitions, as shown below, you'll see that a square containing 4 elements is created at each of their intersections.
When these 9 squares are combined and segregated to create a 6 x 6 (36 element) square, and this square is compared to the Vedic Square minus its 3's, 6's and 9's
(the result dubbed "Imaginary Square"), you'll discover that they share identical vertical and horizontal secquences, though in a different order (alternating +2 and -2 from each other), and that these can be easily made to match exactly by applying a simple function multiplier, as described and illustrated later below.
This graphic illustrates how the Imaginary Square is distilled from the Vedic Square (aka Digital Root Multiplication Table):
Now, if you construct a 4 x 4 square from 16 Imaginary Squares, lo and behold you create a matrix that serves as a digital root calculator, possesses origin
symmetry, has palindromic diagonals and all of its rows and columns sum to 108 and possess 12 bi-lateral sums totaling 9, and the {1,4,7} and {2,5,8} members
of the Trinity of Triangles parse along the principal diagonals, which together have their own dance of bi-lateral 9's ... Sound familiar?
Here it is:
The Amazing Number 89
Before leaving this subject, it's worth noting that 89, the 24th prime number, the 24th element in the set of natural numbers not divisible by 2, 3 and 5, and the last
(i.e., 24th) element operated on in the Magic Mirror Matrix, has other fascinating attributes:
• It's the 11th Fibonacci number (11 + 89 = 100 and, interestingly, 11 in a mod 90 circle has a radius of 44° and the reciprocal of 89 has 44 digits);
• It's the 5th Fibonacci prime;
• It is 100 - 10 -1;
• As stated previously, the number of prime numbers between 1 and 892 (7921) is exactly 1000 [and for the record, there are exactly 111,000 primes between (360 x 2-1)2 and (360 x 4-1)2, i.e., between 7192 and 14392. Both 719 & 1439 are prime and both are ≌ 89 (modulo 90). Also, the number of primes between 892 (7921) and 3892 (151321) is exactly 12960 = 36 x 360, while 12960/30 = 432, a number possessing special significance, as we discuss on our page devoted to twin primes.
• Astoundingly, given there are precisely 1000 prime numbers between 1 and 892 (7921): (89 x 91) - (89 + 91) = 7919, which happens to be the 1000th prime number, not to mention that 8 x 9 x 10 x 11 + 1 = 7921 = 360 x 22 + 1 = 892;
• 89 = (892 + 89) / 360 x 4;
• f(x) = 360x ± 89 with inputs, x, that give prime results: {1, 2, 8, 12, 23, 30, 35, ...} (the first 14 results satifying the function where both outputs are prime, follow):
1 × 360 + 89 = 449 (prime); 1 × 360 - 89 = 271 (prime);
2 × 360 + 89 = 809 (prime); 2 × 360 - 89 = 631 (prime);
8 × 360 + 89 = 2969 (prime); 8 × 360 - 89 = 2791 (prime);
12 × 360 + 89 = 4409 (prime); 12 × 360 - 89 = 4231 (prime);
23 × 360 + 89 = 8369 (prime); 23 × 360 - 89 = 8191 (prime);
30 × 360 + 89 = 10889 (prime); 30 × 360 - 89 = 10711 (prime);
35 × 360 + 89 = 12689 (prime); 35 × 360 - 89 = 12511 (prime);
43 × 360 + 89 = 15569 (prime); 43 × 360 - 89 = 15391 (prime);
49 × 360 + 89 = 17729 (prime); 49 × 360 - 89 = 17551 (prime);
50 × 360 + 89 = 18089 (prime); 50 × 360 - 89 = 17911 (prime);
56 × 360 + 89 = 20249 (prime); 56 × 360 - 89 = 20071 (prime);
76 × 360 + 89 = 27449 (prime); 76 × 360 - 89 = 27271 (prime);
77 × 360 + 89 = 27809 (prime); 77 × 360 - 89 = 27631 (prime);
93 × 360 + 89 = 33569 (prime); 93 × 360 - 89 = 33391 (prime);
...
• It's the smallest positive integer (and prime, for that matter) whose square and cube are both prime when their digits are reversed;
• The decimal expansion of 89's reciprocal, which can be derived additively from the Fibonacci sequence, is exactly the same as the decimal expansion of the
Fibonacci number it is indexed to divided by 89;
• It's the smallest composite-digit prime and smallest circular prime;
• 9+8+7+6+5+4+3+2+1+2+3+4+5+6+7+8+9 = 89;
• 89/92 = 1.0987654321;
• 89 and its reversal require the most reversals and additions to become palindromic (steps required = 24; there's that number again!);
• As mentioned above, the decimal expansion of 89's reciprocal (1/89) is encoded in the Fibonacci sequence: Thus, Fibonacci numbers (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.) sum to the reciprocal of 89 when tabulated in a column for addition purposes, with the decimal point shifted one place to the right for each Fibonacci number in turn,
as illustrated here; and, no doubt related;
• The decimal expansion of 89's reciprocal has 22 numerical reductions totaling 9 each to create perfect cascading symmetry, not to
mention the center midpoint (between the 22nd & 23rd digits) splits number 89:

Another way to present this assembly line of 9's is to add the first 22 digits of 89's decimal expansion to its last 22 digits, like this:

And then there are these provocative results regarding the delta diferences in prime counts for numbers congruent to 89 (mod 90) squared, that speak for themselves (We are currently compiling many other examples like these.):
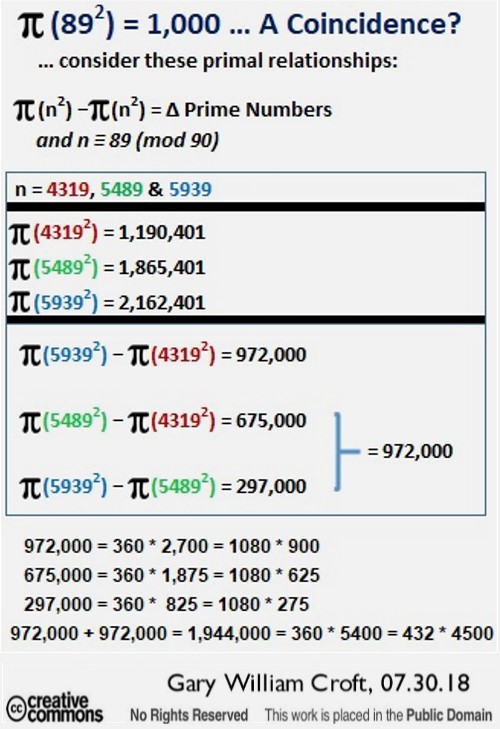
[We should add that 972,000 + 972,000 = 1,944,000, while 1,944,000/360 = 5400, and 1,944,000/432 = 4500 (see note about the number 432, below).]
Also note that number 109, like 89 a prime number, has properties in its decimal expansion similar to 89's. For more information about the numbers 89 and 109, or for that matter any specific prime number you'd like to check out, an excellent source on the internet is Prime Curios. The mathematical relationship between these two numbers is explored on our page devoted to twin primes where you'll learn that [89,109] are 'Fibonacci Twins'.
[Note: There's one more dimension of this matrix that will no doubt be received as speculation of the bubble-off-center kind,
but consider this: The four perimeter sequences of digital roots used to factorize the Magic Mirror Matrix equal 4 x 108 = 432. It turns out
432 is a number possessing great import. For example, 432 has been declared by mystics and scientists alike to be the "frequency of the universe" to which the "music of the spheres" is tuned. 4322 closely approximates the speed of light in a vacuum. When we find a connection between primes 89 and 109 (both possessing the basis of the Fibonacci sequence in the decimal expansions of their reciprocals) and their twin prime candidates to 360 vis-a-vis 432, we are intrigued. But when we discover that the sum of digital roots of the 96 elements in the set of natural numbers not divisible by 2, 3 or 5 between 0 and 360 = 432, not to mention the sum of the digital roots of the Fibonacci numbers and Lucas numbers indexed to these 96 elements also equal 432, we are astounded (In fact, if you expand the Magic Mirror Matrix to encompass the digital roots of the first 96 elements of our domain, making 359 the higest number factorized, all columns and rows equal 432. And, by the way, the values of the 96 elements themselves sum to 1080 = 3 x 360.). And then there's this: The first 89 digits to the right of the decimal point in pi (.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482) sum to 432. Is this a coincidence? Or is it a clue that there might be hidden order in pi's decimialization after all(?). Also consider this: 431 ≌ 7919 mod 242 (7919 being the 1000th prime number); 432 ≌ 7920 mod 242 (7920 = 2 x 11 x 360); 433 ≌ 892 mod 242. And, by the way, 431 and 433 are twin primes, while 431 + 433 = 864 = 24 x 36.
We detail other interesting aspects of 432 in relation to prime numbers in 360° cycles, as well as the significance of 24-beat periodicity, which lies at the heart of the domain's factorization sequencing, in our discussion of twin primes. So does one dare entertain the possibility that the Magic Mirror Matrix is a geoarithmetric representation of the frequency of the cosmos ... without being relegated to the lunatic fringe? It makes sense that prime number factorization / sequencing would be at its heart, and that the first rotation, when the matrix is viewed as a modulo 90 factorization spiral, represents the first 1000 prime numbers. Don't laugh. As a philosopher or action scientist might say, be open to discomfirmability.]